本文是2019年机器学习课程学习笔记,分为7个章节,分别是引言、模型评估与选择、线性模型、决策树、支持向量机、神经网络、朴素贝叶斯。各章节的写作结构是从问题出发,然后介绍各算法理论知识,最终编程实现算法。编程软件为R语言。详细数据及代码见ML2019 。
数学虐我千百遍,我待数学如初恋;统计虐我千百遍,我待统计如初恋;概率虐我千百遍,我待概率如初恋;线模虐我千百遍,我待线模如初恋。
老师讲完课后,纳尼,老师这节课讲了啥,怎么听得云里雾里的,哎,算了吧,自己下去看吧。
当我捧起讲义和课本时,我看了一节,咦,这节讲了点啥,咋啥都没看懂呢?恩,没事,看不懂就再看一遍。好,我又看了一遍,这回有点眉目了,还是没太懂。恩,不着急,那就再看一遍。于是,我又看了一 遍,恩,这回懂得差不多了,还剩个别细节不太懂。
看懂了那就做题吧,于是我满怀信心翻开了习题,准备大干一场。咦,第一题啥意思,它要干啥,完全不懂啊,完全不知道它要干啥。没事,再念一遍,再想想。恩,这回看完,想了想,知道它要考啥了,可是还是不会做啊。不着急,翻翻讲义看看书再想想,恩,看完了还是不会做。恩,没事,先做下一道,然后再做这道题,说不定就会做了…
第二天,我又捧起了习题,大眼瞪小眼,还是不会做,我好晕啊。没事,不是有答案嘛,看看答案。哇!还好,答案我还能看懂。—— By XZZ
机器学习是对能通过经验自动改进的计算机算法的研究。它是一门多领域的交叉学科,涉及概率论、统计学、逼近论、凸分析、算法复杂度理论论等多门学科。它专门研究计算机怎样模拟或实现人类的学习行为,以获取新的知识或技能,重新组织已有的知识结构使之不断改善自身的性能。它是人工智能的核心,是使计算机具有智能的根本途径,其应用遍及人工智能的各个领域,它主要使用归纳、综合而不是演绎。它的应用已遍及人工智能的各个分支,如专家系统、自动推理、自然语言理解、模式识别、计算机视觉、智能机器人等领域。
机器学习是人工智能研究较为年轻的分支,它的发展过程大体上分为四个时期。第一阶段是20世纪50年代中叶到60年代中叶,属于热烈时期。在这个时期,所研究的是“没有知识”的学习,即“无知”学习。其研究目标是各类自组织系统和自适应系统,其主要研究方法是不断修改系统的控制参数和改进系统的执行能力,不涉及与具体任务有关的知识。本阶段的代表性工作是:塞缪尔(Samuel)的下棋程序。但这种学习的结果远不能满足人们对机器学习系统的期望。第二阶段是在60年代中叶到70年代中叶,被称为机器学习的冷静时期。本阶段的研究目标是模拟人类的概念学习过程,并采用逻辑结构或图结构作为机器内部描述。本阶段的代表性工作有温斯顿(Winston)的结构学习系统和海斯罗思(Hayes-Roth)等的基本逻辑的归纳学习系统。第三阶段从20世纪70年代中叶到80年代中叶,称为复兴时期。在此期间,人们从学习单个概念扩展到学习多个概念,探索不同的学习策略和方法,且在本阶段已开始把学习系统与各种应用结合起来,并取得很大的成功,促进机器学习的发展。1980年,在美国的卡内基—梅隆(CMU)召开了第一届机器学习国际研讨会,标志着机器学习研究已在全世界兴起。
机器学习一般根据处理的数据是否存在人为标注主要分为监督学习和无监督学习。监督学习用有标签的数据作为最终学习目标,通常学习效果好,但获取有标签数据的代价是昂贵的,无监督学习相当于自学习或自助式学习,便于利用更多的数据,同时可能会发现数据中存在的更多模式的先验知识(有时会超过手工标注的模式信息),但学习效率较低。二者的共性是通过建立数学模型为最优化问题进行求解,通常没有完美的解法。
监督学习的数据集包括初始训练数据和人为标注目标,希望根据标注特征从训练集数据中学习到对象划分的规则,并应用此规则在测试集数据中预测结果,输出有标记的学习方式。因此,监督学习的根本目标是训练机器学习的泛化能力。监督学习的典型算法有:逻辑回归、多层感知机、卷积神经网络等;典型应用有:回归分析、任务分类等。
无监督学习用于处理未被分类标记的样本集数据并且事先不需要进行训练,希望通过学习寻求数据间的内在模式和统计规律,从而获得样本数据的结构特征。因此,无监督学习的根本目标是在学习过程中根据相似性原理进行区分"无监督学习更近似于人类的学习方式,被誉为:人工智能最有价值的地方。无监督学习的典型算法有自动编码器、受限玻尔兹曼机、深度置信网络等;典型应用有:聚类和异常检测等。
本文分为7个章节,分别是引言、模型评估与选择、线性模型、决策树、支持向量机、神经网络、朴素贝叶斯。第二章模型评估与选择主要介绍了查准率、查全率、PR曲线与ROC曲线。第三章线性模型分为两部分,分别是逻辑回归与线性判别分析,并且分别介绍了梯度下降法、牛顿法求解逻辑回归参数值。第四章决策树介绍了经典的ID3、C4.5与CART算法。第五章支持向量机介绍了支持向量机分类与支持向量机回归,其中又详细介绍了支持向量机分类的原问题与对偶问题、高斯核以及支持向量机多分类问题。第六章神经网络介绍了BP反向传播算法估计各神经元参数值与随机梯度下降算法。第七章讲解了朴素贝叶斯算法。各章节的写作结构是从问题出发,然后介绍各算法理论知识,最终编程实现算法。编程软件为R语言。
构造一个包含1000个样本的数据集,按照某种模型对样本排序,前500个样本中正例(取值1)占90%, 后500个样本中反例(取值0)占80%。
1 2 pred <- c (round (runif(500 ) / 2 + 0.45 ), round (runif(500 ) / 2 + 0.10 ))
## [1] 1 1 1 1 1 1
## [1] 1 0 0 1 0 0
## [1] 0.551
试给出该模型的P P P R R R R O C ROC R O C
P P P R R R 对于二分类问题,可将样例根据其真实类别与学习器预测类别的组合划分为真正例(true positive)、 假正例(false positive)、真反例(true negative)、假反例(false negative)四种情形,对应的混淆矩阵如下所示。
Predict1
Predict0
Act1
TP
FN
Act0
FP
TN
查准率P P P R R R
P = T P T P + F P P=\frac {TP} {TP + FP}
P = T P + F P T P
R = T P T P + F N R=\frac {TP} {TP + FN}
R = T P + F N T P
F 1 F1 F 1
F 1 = 2 × P × R P + R F1 = \frac {2\times P\times R} {P + R}
F 1 = P + R 2 × P × R
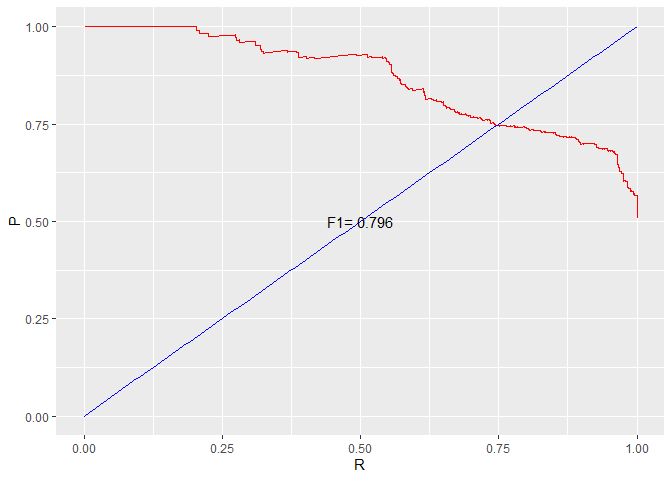
我们根据学习器的预测结果对样例进行排序,排在最前面的是学习器认为“最可能”是正例的样本,排在最后面的是学习器认为“最不可能”的正例样本。按此顺序逐个把样本作为正例预测,每次可计算出查全率与查准率。以查准率为纵轴,查全率为横轴作图,就可以得到“P P P R R R
注意 :在上述代码中我们构建的pred已经是按照预测概率排序后的数据集(真实数据的标签 ),所以在接下来我们只需要利用for循环计算每一次的P P P R R R
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 PRCurve <- function (pred){ m <- length (pred) P <- R <- rep (0 , m) for (i in 1 : m){ predi <- c (rep (1 , i), rep (0 , m - i)) tab <- table(predi, pred) if (i != m){ P[i] <- tab[2 , 2 ] / (tab[2 , 1 ] + tab[2 , 2 ]) R[i] <- tab[2 , 2 ] / (tab[1 , 2 ] + tab[2 , 2 ]) }else { P[i] <- tab[1 , 2 ] / (tab[1 , 1 ] + tab[1 , 2 ]) R[i] <- tab[1 , 2 ] / tab[1 , 2 ] } } F1 <- 2 * P * R / (P + R) bound <- which(F1 == max (F1)) F1 <- max (F1) return (list (P = P, R = R, F1 = F1, bound = bound)) } PR <- PRCurve(pred) P <- PR$P R <- PR$R F1 <- PR$F1 bound <- PR$bound
1 2 3 4 5 6 7 8 library(ggplot2) da1 <- data.frame(P = P, R = R) da2 <- data.frame(x = seq(0 , 1 , 0.01 ), y = seq(0 , 1 , 0.01 )) ggplot(data = da1, aes(x = R, y = P)) + geom_line(colour = "red" ) + xlim(0 , 1 ) + ylim(0 , 1 ) + geom_line(data = da2, aes(x = x, y = y), colour = "blue" ) + geom_text(data = data.frame(x = 0.5 , y = 0.5 ), aes(x = x, y = y, label = paste("F1=" , round (F1, 3 ))))
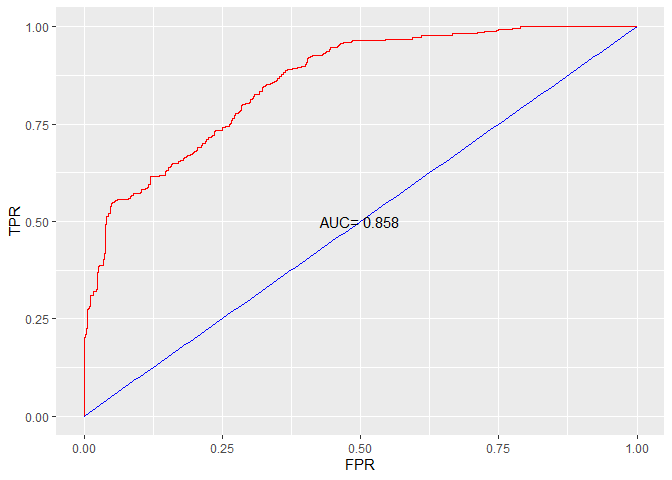
RO C 曲线R O C ROC R O C P P P R R R R O C ROC R O C
T P R = T P T P + F N TPR = \frac {TP} {TP + FN}
T P R = T P + F N T P
F P R = T P T N + F P FPR = \frac {TP} {TN + FP}
F P R = T N + F P T P
若一个机器学习的R O C ROC R O C R O C ROC R O C A U C AUC A U C R O C ROC R O C
A U C = 1 2 ∑ i = 1 m − 1 ( x i + 1 − x i ) ( y i + y i + 1 ) AUC = \frac{1}{2} \sum_{i=1}^{m-1} (x_{i+1} - x_i)(y_i + y_{i+1})
A U C = 2 1 i = 1 ∑ m − 1 ( x i + 1 − x i ) ( y i + y i + 1 )
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 ROCCurve <- function (pred){ m <- length (pred) TPR <- FPR <- rep (0 , m + 1 ) AUC <- 0 for (i in 1 : (m - 1 )){ predi <- c (rep (1 , i), rep (0 , m - i)) tab <- table(predi, pred) TPR[i + 1 ] <- tab[2 , 2 ] / (tab[1 , 2 ] + tab[2 , 2 ]) FPR[i + 1 ] <- tab[2 , 1 ] / (tab[1 , 1 ] + tab[2 , 1 ]) AUC <- AUC + (1 /2 ) * (TPR[i + 1 ] + TPR[i]) * (FPR[i + 1 ] - FPR[i]) } TPR[m + 1 ] <- 1 FPR[m + 1 ] <- 1 AUC <- AUC + (1 /2 ) * (TPR[m + 1 ] + TPR[m]) * (FPR[m + 1 ] - FPR[m]) return (list (TPR = TPR, FPR = FPR, AUC = AUC)) } ROC <- ROCCurve(pred) TPR <- ROC$TPR FPR <- ROC$FPR AUC <- ROC$AUC
1 2 3 4 5 6 7 8 library(ggplot2) da1 <- data.frame(TPR = TPR, FPR = FPR) da2 <- data.frame(x = seq(0 , 1 , 0.01 ), y = seq(0 , 1 , 0.01 )) ggplot(data = da1, aes(x = FPR, y = TPR)) + geom_line(colour = "red" ) + xlim(0 , 1 ) + ylim(0 , 1 ) + geom_line(data = da2, aes(x = x, y = y), colour = "blue" ) + geom_text(data = data.frame(x = 0.5 , y = 0.5 ), aes(x = x, y = y, label = paste("AUC=" , round (AUC, 3 ))))
模型评估与选择的方法还有很多种,如错误率与精度、代价敏感错误率与代价曲线、比较检验、偏差与方差等。在模型评估过程中应因地制宜,根据模型本身制定合适的评价标准。当负例样本占样本集比例较小时(如5%)就不能使用错误率衡量模型的好坏。
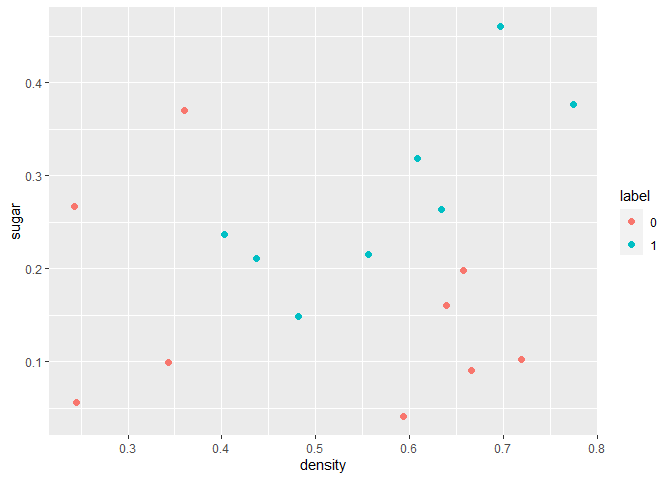
从csv文件中读取西瓜数据,并进行展示。
1 2 wmda <- read.csv(file = "Test2/data/西瓜数据3.0a.csv" ) wmda$label <- as.factor(wmda$label)
1 knitr::kable(head(wmda))
idx
density
sugar
label
1
0.697
0.460
1
2
0.774
0.376
1
3
0.634
0.264
1
4
0.608
0.318
1
5
0.556
0.215
1
6
0.403
0.237
1
## density sugar label
## Min. :0.2430 Min. :0.0420 0:9
## 1st Qu.:0.4030 1st Qu.:0.1030 1:8
## Median :0.5930 Median :0.2110
## Mean :0.5326 Mean :0.2128
## 3rd Qu.:0.6570 3rd Qu.:0.2670
## Max. :0.7740 Max. :0.4600
1 2 ggplot(data = wmda, aes(x = density, y = sugar, color = label)) + geom_point(size = 2.0 , shape = 16 )
逻辑回归是处理典型分类问题的,如判断一个邮件是否为垃圾邮件(Spam / not Spam)。逻辑回归与线性回归直观区别是:线性回归将预测值映射到了实数集(h θ ( x ) h_{\theta}(x) h θ ( x ) 0 ≤ h θ ( x ) ≤ 1 0\le h_{\theta}(x) \le 1 0 ≤ h θ ( x ) ≤ 1
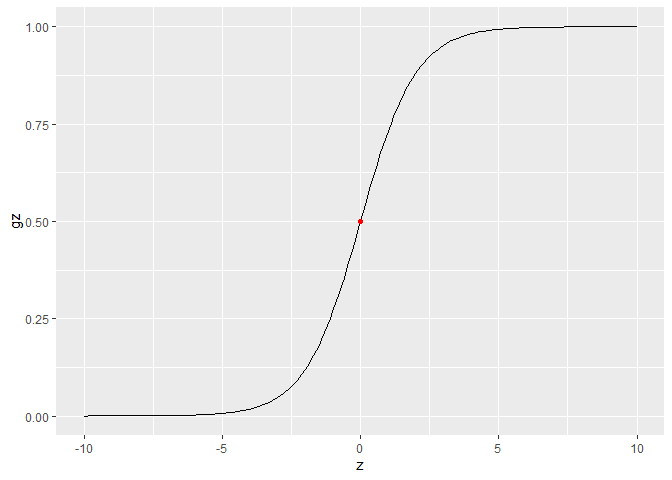
假设表示(Hypothesis Representation)代表当有一个实际问题时,我们用什么样的方程表示。逻辑回归是想实现0 ≤ h θ ( x ) ≤ 1 0\le h_{\theta}(x) \le 1 0 ≤ h θ ( x ) ≤ 1
h θ ( x ) = g ( θ T x ) h_\theta(x) = g(\theta ^T x)
h θ ( x ) = g ( θ T x )
g ( z ) = 1 1 + e − z g(z)=\dfrac{1}{1+e^{-z}}
g ( z ) = 1 + e − z 1
h θ ( x ) = P ( y = 1 ∣ x ; θ ) h_\theta(x)=P(y=1|x;\theta)
h θ ( x ) = P ( y = 1 ∣ x ; θ )
h θ ( x ) h_\theta(x) h θ ( x ) y = 1 y=1 y = 1 x x x θ \theta θ
假设当h θ ( x ) h_\theta(x) h θ ( x ) y = 1 y=1 y = 1 h θ ( x ) h_\theta(x) h θ ( x ) y = 0 y=0 y = 0 h θ ( x ) = 0 . 5 h_\theta(x)=0.5 h θ ( x ) = 0 . 5 θ T x = 0 \theta^Tx = 0 θ T x = 0 θ = [ − 3 ; 1 ; 1 ] \theta=[-3; 1; 1] θ = [ − 3 ; 1 ; 1 ] x 1 + x 2 = 3 x_1+x_2 = 3 x 1 + x 2 = 3
非线性决策边界是指当假设函数h θ ( x ) h_\theta(x) h θ ( x ) h θ ( x ) = g ( θ 0 + θ 1 x 1 + θ 2 x 2 + θ 3 x 1 2 + θ 4 x 2 2 ) h_\theta(x) = g(\theta_0 + \theta_1x_1 + \theta_2x_2 + \theta_3x_1^2 + \theta_4x_2^2) h θ ( x ) = g ( θ 0 + θ 1 x 1 + θ 2 x 2 + θ 3 x 1 2 + θ 4 x 2 2 ) θ = [ − 1 ; 0 ; 0 ; 1 ; 1 ] \theta=[-1; 0;0;1;1] θ = [ − 1 ; 0 ; 0 ; 1 ; 1 ] x 1 2 + x 2 2 = 0 x_1^2+x_2^2=0 x 1 2 + x 2 2 = 0
假设测试集为{ ( x ( 1 ) , y ( 1 ) ) , ( x ( 2 ) , y ( 2 ) ) , . . . , ( x ( m ) , y ( m ) ) } \{(x^{(1)},y^{(1)}), (x^{(2)},y^{(2)}), ... , (x^{(m)},y^{(m)})\} { ( x ( 1 ) , y ( 1 ) ) , ( x ( 2 ) , y ( 2 ) ) , . . . , ( x ( m ) , y ( m ) ) } x ∈ [ x 0 ; x 1 ; . . . ; x n ] x\in[x_0;x_1;...;x_n] x ∈ [ x 0 ; x 1 ; . . . ; x n ] x 0 = 1 x_0=1 x 0 = 1 y ∈ { 0 , 1 } y\in\{0,1\} y ∈ { 0 , 1 }
J θ = 1 m ∑ i = 1 m 1 2 ( h θ ( x ( i ) ) − y ( i ) ) 2 J_\theta = \dfrac{1}{m}\sum_{i=1}^m \dfrac{1}{2}(h_\theta(x^{(i)})-y^{(i)})^2
J θ = m 1 i = 1 ∑ m 2 1 ( h θ ( x ( i ) ) − y ( i ) ) 2
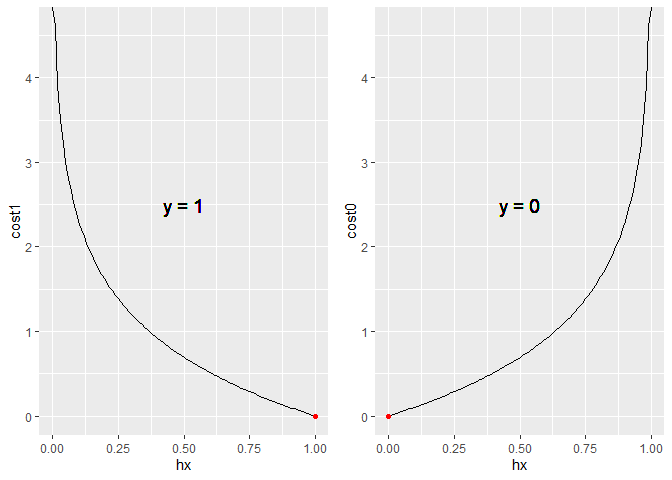
c o s t ( h θ ( x ) , y ) = 1 2 ( h θ ( x ) − y ) 2 cost(h_\theta(x), y)=\dfrac{1}{2}(h_\theta(x)-y)^2
c o s t ( h θ ( x ) , y ) = 2 1 ( h θ ( x ) − y ) 2
然而这个函数在逻辑回归里是θ \theta θ
c o s t ( h θ ( x ) , y ) = { − l o g ( h θ ( x ) ) , i f y = 1 − l o g ( 1 − h θ ( x ) ) , i f y = 0 cost(h_\theta(x), y) =
\begin{cases}
-log(h_\theta(x)), & {if }y{=1} \\
-log(1-h_\theta(x)), & {if }y{=0}
\end{cases}
c o s t ( h θ ( x ) , y ) = { − l o g ( h θ ( x ) ) , − l o g ( 1 − h θ ( x ) ) , i f y = 1 i f y = 0
简化形式为:
c o s t ( h θ ( x ) , y ) = − y l o g ( h θ ( x ) ) − ( 1 − y ) l o g ( 1 − h θ ( x ) ) cost(h_\theta(x), y) = -ylog(h_\theta(x)) - (1-y)log(1-h_\theta(x))
c o s t ( h θ ( x ) , y ) = − y l o g ( h θ ( x ) ) − ( 1 − y ) l o g ( 1 − h θ ( x ) )
那么逻辑回归的代价函数就为:
J θ = 1 m ∑ i = 1 m ( − y ( i ) l o g ( h θ ( x ( i ) ) ) − ( 1 − y ( i ) ) l o g ( 1 − h θ ( x ( i ) ) ) ) J_\theta = \dfrac{1}{m}\sum_{i=1}^m (-y^{(i)}log(h_\theta(x^{(i)})) -
(1-y^{(i)})log(1-h_\theta(x^{(i)})))
J θ = m 1 i = 1 ∑ m ( − y ( i ) l o g ( h θ ( x ( i ) ) ) − ( 1 − y ( i ) ) l o g ( 1 − h θ ( x ( i ) ) ) )
上式来自于极大似然估计,具体推导过程如下:
从假设表示中有提到h θ ( x ) h_\theta(x) h θ ( x ) y = 1 y=1 y = 1 x x x θ \theta θ θ \theta θ
似然函数为:
L = ∏ i = 1 m h θ ( x ( i ) ) Y ( i ) ( 1 − h θ ( x ( i ) ) ) 1 − Y ( i ) L=\prod_{i=1}^m h_\theta(x^{(i)})^{Y^{(i)}} (1-h_\theta(x^{(i)}))^{1-Y^{(i)}}
L = i = 1 ∏ m h θ ( x ( i ) ) Y ( i ) ( 1 − h θ ( x ( i ) ) ) 1 − Y ( i )
l n L = ∑ i = 1 m Y ( i ) ( l n ( h θ ( x ( i ) ) ) ) + ( 1 − Y ( i ) ) ( l n ( 1 − h θ ( x ( i ) ) ) ) lnL = \sum_{i=1}^m Y^{(i)}(ln(h_\theta(x^{(i)}))) + (1-Y^{(i)})(ln(1- h_\theta(x^{(i)})))
l n L = i = 1 ∑ m Y ( i ) ( l n ( h θ ( x ( i ) ) ) ) + ( 1 − Y ( i ) ) ( l n ( 1 − h θ ( x ( i ) ) ) )
求似然函数的最大值等价于求J θ J_\theta J θ
上节中已知J θ J_\theta J θ θ \theta θ
J θ = 1 m ∑ i = 1 m ( − y ( i ) log ( h θ ( x ( i ) ) ) − ( 1 − y ( i ) ) log ( 1 − h θ ( x ( i ) ) ) ) = 1 m ∑ i = 1 m − y ( i ) ( log ( h θ ( x ( i ) ) ) − log ( 1 − h θ ( x ( i ) ) ) ) − log ( 1 − h θ ( x ( i ) ) ) = 1 m ∑ i = 1 m − y ( i ) log h θ ( x ( i ) ) 1 − h θ ( x ( i ) ) − log ( 1 − h θ ( x ( i ) ) ) = 1 m ∑ i = 1 m − y ( i ) ( θ T x ( i ) ) + log ( 1 + e θ T x ( i ) ) \begin{aligned}
J_{\theta} &=\frac{1}{m} \sum_{i=1}^{m}\left(-y^{(i)} \log \left(h_{\theta}\left(x^{(i)}\right)\right)-\left(1-y^{(i)}\right) \log \left(1-h_{\theta}\left(x^{(i)}\right)\right)\right) \\
&=\frac{1}{m} \sum_{i=1}^{m}-y^{(i)}\left(\log \left(h_{\theta}\left(x^{(i)}\right)\right)-\log \left(1-h_{\theta}\left(x^{(i)}\right)\right)\right)-\log \left(1-h_{\theta}\left(x^{(i)}\right)\right) \\
&=\frac{1}{m} \sum_{i=1}^{m}-y^{(i)} \log \frac{h_{\theta}\left(x^{(i)}\right)}{1-h_{\theta}\left(x^{(i)}\right)}-\log \left(1-h_{\theta}\left(x^{(i)}\right)\right) \\
&=\frac{1}{m} \sum_{i=1}^{m}-y^{(i)}\left(\theta^{T} x^{(i)}\right)+\log \left(1+e^{\theta^{T} x^{(i)}}\right)
\end{aligned}
J θ = m 1 i = 1 ∑ m ( − y ( i ) log ( h θ ( x ( i ) ) ) − ( 1 − y ( i ) ) log ( 1 − h θ ( x ( i ) ) ) ) = m 1 i = 1 ∑ m − y ( i ) ( log ( h θ ( x ( i ) ) ) − log ( 1 − h θ ( x ( i ) ) ) ) − log ( 1 − h θ ( x ( i ) ) ) = m 1 i = 1 ∑ m − y ( i ) log 1 − h θ ( x ( i ) ) h θ ( x ( i ) ) − log ( 1 − h θ ( x ( i ) ) ) = m 1 i = 1 ∑ m − y ( i ) ( θ T x ( i ) ) + log ( 1 + e θ T x ( i ) )
∂ ∂ θ j J θ = 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) \frac{\partial}{\partial \theta_{j}} J_{\theta}=\frac{1}{m} \sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right) x_{j}^{(i)}
∂ θ j ∂ J θ = m 1 i = 1 ∑ m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i )
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 sigmoid <- function (z){ return (1 / (1 + exp (-z))) } gradientDescent <- function (X, y, theta, alpha, num_iters){ m <- length (y) J.history <- rep (0 , num_iters) for (i in 1 :num_iters){ theta <- theta - (1 /m) * (t(X) %*% (sigmoid(X %*% theta) - y)) J.history[i] <- (1 /m) * sum (-y * log (sigmoid(X %*% theta)) - (1 -y) * (log (1 - sigmoid(X %*% theta)))) } return (list (theta = theta, J = J.history)) } X <- as.matrix(wmda[, 2 :3 ]) X <- cbind(1 , X) y <- as.matrix(as.numeric (as.character (wmda$label))) initial_theta <- matrix(rep (0 , 3 ), ncol = 1 ) alpha <- 0.1 Ret <- gradientDescent(X, y, initial_theta, alpha, num_iters = 5000 )
## [1] -4.419850 3.151482 12.495210
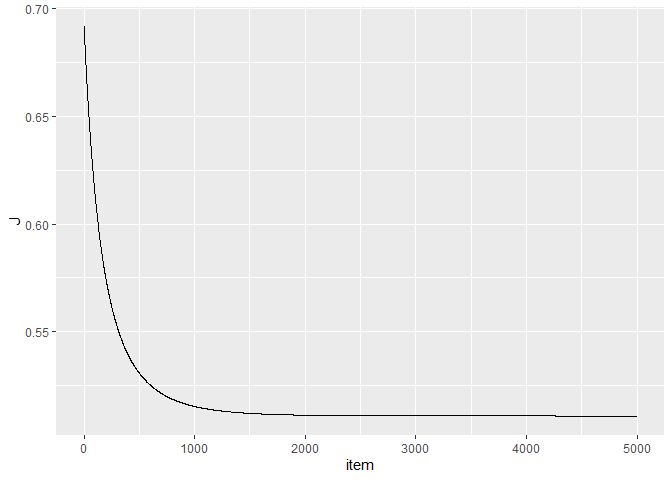
1 2 ggplot(data = data.frame(item = 1 :length (Ret$J), J = Ret$J), aes(x = item, y = J)) + geom_line()
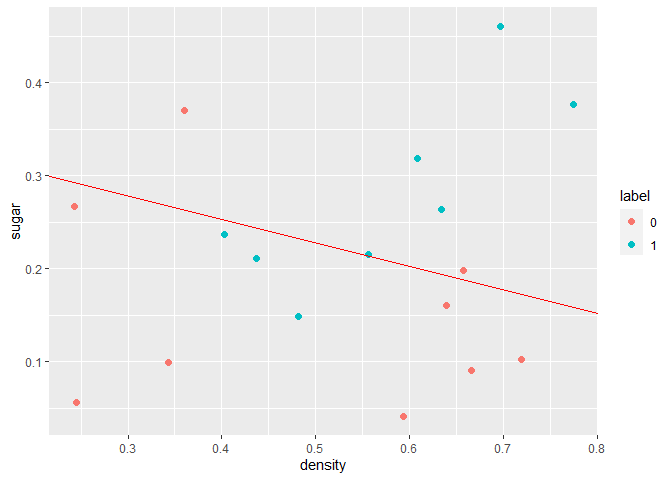
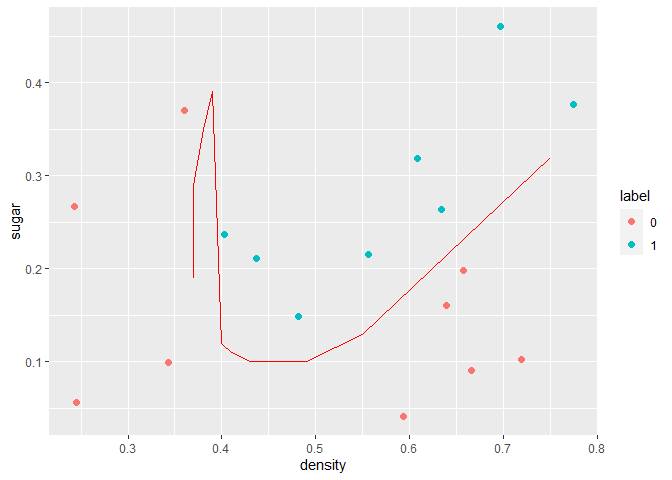
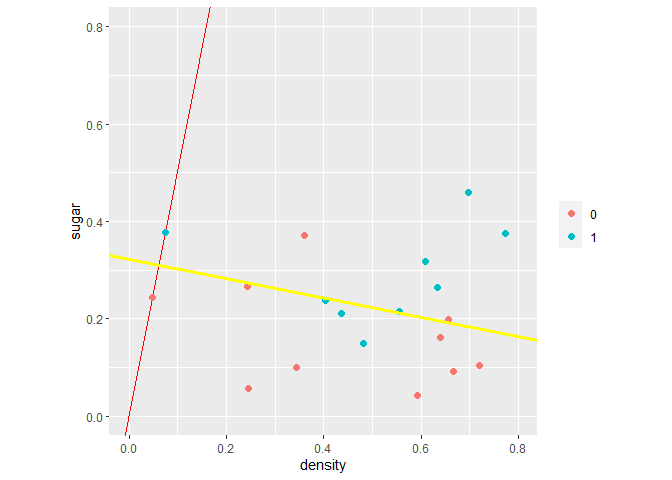
1 2 3 4 5 ggplot(data = wmda, aes(x = density, y = sugar, color = label)) + geom_point(size = 2.0 , shape = 16 ) + geom_abline(slope = -Ret$theta[2 ] / Ret$theta[3 ], intercept = -Ret$theta[1 ]/Ret$theta[3 ], color = "red" )
从上图可以看到,逻辑回归对西瓜集的分类是较差的。我们也可以直观的看到西瓜集是线性不可分的!所以这里引入了高阶特征,构建非线性边界去划分西瓜集。构建方法为选择最高次数,将两变量映射到高阶上形成新特征。例如构建最高幂次为6的特征,此时会产生新特征如:x 1 6 x_1^6 x 1 6 x 2 6 x_2^6 x 2 6 x 1 5 x 2 x_1^5x_2 x 1 5 x 2 x 1 x 2 x_1x_2 x 1 x 2 x 2 x_2 x 2 x 1 x_1 x 1
1 2 3 4 5 6 7 8 9 10 11 12 13 14 mapFeature <- function (x1, x2, degree){ df <- matrix(1 , nrow = length (x1)) for (i in 1 :degree){ for (j in 0 :i){ x <- x1^(i - j) * x2^(j) df <- cbind(df, x) } } return (df) } x1 <- wmda$density x2 <- wmda$sugar X <- mapFeature(x1, x2, 6 )
如果我们有太多特征,那么通过训练集得到的模型很可能会过拟合,使得模型对新样本的预测值差。为了解决过拟合的问题,提出了正则化(Regularization)。过拟合的问题还可以通过手工选择特征或者通过算法(如PCA)来减少特征数。
正则化的思想是控制参数θ j \theta_j θ j θ 0 \theta_0 θ 0
J θ = 1 m ∑ i = 1 m ( − y ( i ) l o g ( h θ ( x ( i ) ) ) − ( 1 − y ( i ) ) l o g ( 1 − h θ ( x ( i ) ) ) ) + λ 2 m ∑ j = 1 n θ j 2 J_\theta = \dfrac{1}{m}\sum_{i=1}^m (-y^{(i)}log(h_\theta(x^{(i)})) -
(1-y^{(i)})log(1-h_\theta(x^{(i)}))) + \dfrac{\lambda}{2m} \sum_{j=1}^n \theta_j^2
J θ = m 1 i = 1 ∑ m ( − y ( i ) l o g ( h θ ( x ( i ) ) ) − ( 1 − y ( i ) ) l o g ( 1 − h θ ( x ( i ) ) ) ) + 2 m λ j = 1 ∑ n θ j 2
∂ ∂ θ j J θ = 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) + λ m θ j \dfrac{\partial}{\partial \theta_j} J_\theta = \dfrac{1}{m} \sum_{i=1}^m
(h_\theta(x^{(i)}) - y^{(i)})x_j^{(i)} + \dfrac{\lambda}{m} \theta_j
∂ θ j ∂ J θ = m 1 i = 1 ∑ m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) + m λ θ j
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 gradientDescent <- function (X, y, theta, alpha, num_iters, lambda){ m <- length (y) n <- ncol(X) J.history <- rep (0 , num_iters) for (i in 1 :num_iters){ theta[1 ] <- theta[1 ] - (1 /m) * (t(X[, 1 ]) %*% (sigmoid(X %*% theta) - y)) theta[2 :n] <- theta[2 :n] - (1 /m) * (t(X[, 2 :n]) %*% (sigmoid(X %*% theta) - y)) + lambda/m * theta[2 :n] J.history[i] <- (1 /m) * sum (-y * log (sigmoid(X %*% theta)) - (1 -y) * (log (1 - sigmoid(X %*% theta)))) + (lambda/2 /m) * sum (theta[2 :n] ^2 ) } return (list (theta = theta, J = J.history)) } y <- as.matrix(as.numeric (as.character (wmda$label))) initial_theta <- matrix(rep (0 , 28 ), ncol = 1 ) alpha <- 0.1 lambda <- 0 Ret <- gradientDescent(X, y, initial_theta, alpha, num_iters = 100000 , lambda)
## [1] -18.2576688 55.5141514 -10.7170173 -12.4644799 66.1030944 -49.1665058
## [7] -48.6936829 60.3009426 14.7737220 -32.2204811 -50.7437367 44.6194226
## [13] 26.2238727 1.2997743 -15.4884559 -37.5326066 32.8471126 24.1358494
## [19] 9.3827915 -0.7082506 -6.5816698 -21.6262370 25.2981189 19.6096944
## [25] 9.8597332 3.2328093 -0.5628648 -2.6294491
1 2 3 4 5 6 7 8 p <- sigmoid(X %*% Ret$theta) pos <- which(p >= 0.5 ) neg <- which(p < 0.5 ) p[pos] <- 1 p[neg] <- 0 t <- table(p, wmda$label) print(paste("prediction accuracy = " , sum (t) / sum (diag(t)) * 100 , "%" ))
## [1] "prediction accuracy = 100 %"
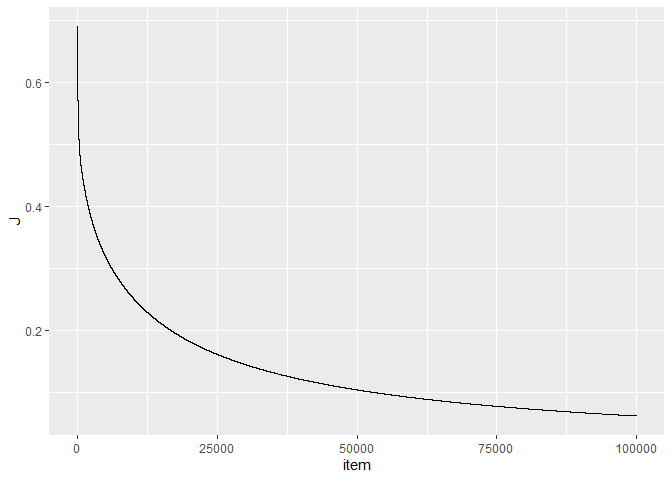
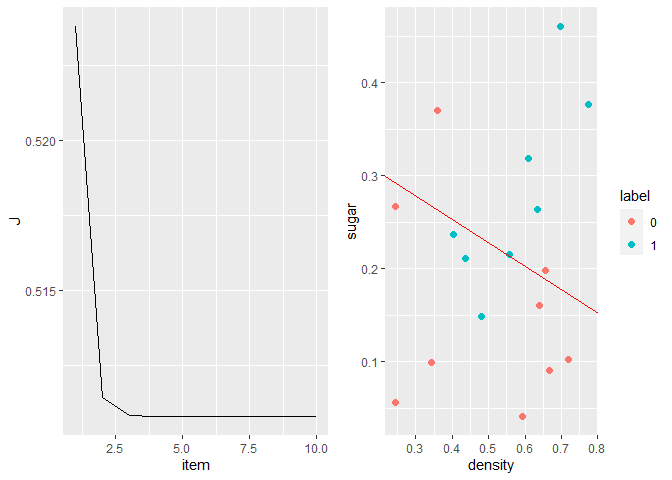
1 2 ggplot(data = data.frame(item = 1 :length (Ret$J), J = Ret$J), aes(x = item, y = J)) + geom_line()
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 x1 <- seq(0 , 0.8 , 0.01 ) x2 <- seq(0 , 0.5 , 0.01 ) x.grad <- data.frame() for (i in x1){ for (j in x2){ x.grad <- rbind(x.grad, c (i, j)) } } colnames(x.grad) <- c ("x1" , "x2" ) X.grad <- mapFeature(x.grad[, 1 ], x.grad[, 2 ], 6 ) p <- sigmoid(X.grad %*% Ret$theta) idx <- which(p < 0.5 +0.01 & p > 0.5 -0.01 ) ggplot(data = wmda, aes(x = density, y = sugar, color = label)) + geom_point(size = 2.0 , shape = 16 ) + geom_line(data = x.grad[idx, ], aes(x = x1, y = x2), colour = "red" )
可以利用One-vs-all算法,创建伪训练集,例如:预测天气(Sunny、Cloudy、Rain、Snow),可以学习四个逻辑回归,判断哪个概率最高,则属于哪一类。
牛顿法主要可以求解方程f ( θ ) = 0 f{(\theta)} = 0 f ( θ ) = 0 f ( x ) = 0 f(x)=0 f ( x ) = 0 x k x_k x k f ( x ) f(x) f ( x ) x k x_k x k
f ( x ) ≈ f ( x k ) + f ′ ( x k ) ( x − x k ) f(x)\approx f(x_k)+f^\prime(x_k)(x-x_k)
f ( x ) ≈ f ( x k ) + f ′ ( x k ) ( x − x k )
令f ( x ) = 0 f(x)=0 f ( x ) = 0
x k + 1 = x k − f ( x k ) f ′ ( x k ) x_{k+1} = x_k - \dfrac{f(x_k)}{f^\prime(x_k)}
x k + 1 = x k − f ′ ( x k ) f ( x k )
在求解代价函数最小化的过程中,我们可以利用牛顿法迭代求解一阶偏导数的解,从而得出参数的估计值。也就是:
θ = θ − J ′ ( θ ) J ′ ′ ( θ ) \theta = \theta - \dfrac{J^\prime{(\theta})}{J''(\theta)}
θ = θ − J ′ ′ ( θ ) J ′ ( θ )
一阶偏导数为:
∂ ∂ θ j J θ = 1 m ∑ t = 1 m ( h θ ( x ( t ) ) − y ( t ) ) x j ( t ) \frac{\partial}{\partial \theta_{j}} J_{\theta}=\frac{1}{m} \sum_{t=1}^{m}\left(h_{\theta}\left(x^{(t)}\right)-y^{(t)}\right) x_{j}^{(t)}
∂ θ j ∂ J θ = m 1 t = 1 ∑ m ( h θ ( x ( t ) ) − y ( t ) ) x j ( t )
二阶偏导数(Hessian Matrix)为n ∗ n n*n n ∗ n
∂ 2 ∂ θ j ∂ θ i J θ = 1 m ∂ ∂ θ i ∑ t = 1 m ( h θ ( x ( t ) ) − y ( t ) ) x j ( t ) = 1 m ∑ t = 1 m x j ( t ) ∂ ∂ θ i h θ ( x ( t ) ) = 1 m ∑ t = 1 m x j ( t ) h θ ( x ( t ) ) ( 1 − h θ ( x ( t ) ) ) ∂ ∂ θ i ( θ T x ( t ) ) = 1 m ∑ t = 1 m x i ( t ) x j ( t ) h θ ( x ( t ) ) ( 1 − h θ ( x ( t ) ) ) \begin{aligned}
\frac{\partial^{2}}{\partial \theta_{j} \partial \theta_{i}} J_{\theta} &=\frac{1}{m} \frac{\partial}{\partial \theta_{i}} \sum_{t=1}^{m}\left(h_{\theta}\left(x^{(t)}\right)-y^{(t)}\right) x_{j}^{(t)} \\
&=\frac{1}{m} \sum_{t=1}^{m} x_{j}^{(t)} \frac{\partial}{\partial \theta_{i}} h_{\theta}\left(x^{(t)}\right) \\
&=\frac{1}{m} \sum_{t=1}^{m} x_{j}^{(t)} h_{\theta}\left(x^{(t)}\right)\left(1-h_{\theta}\left(x^{(t)}\right)\right) \frac{\partial}{\partial \theta_{i}}\left(\theta^{T} x^{(t)}\right) \\
&=\frac{1}{m} \sum_{t=1}^{m} x_{i}^{(t)} x_{j}^{(t)} h_{\theta}\left(x^{(t)}\right)\left(1-h_{\theta}\left(x^{(t)}\right)\right)
\end{aligned}
∂ θ j ∂ θ i ∂ 2 J θ = m 1 ∂ θ i ∂ t = 1 ∑ m ( h θ ( x ( t ) ) − y ( t ) ) x j ( t ) = m 1 t = 1 ∑ m x j ( t ) ∂ θ i ∂ h θ ( x ( t ) ) = m 1 t = 1 ∑ m x j ( t ) h θ ( x ( t ) ) ( 1 − h θ ( x ( t ) ) ) ∂ θ i ∂ ( θ T x ( t ) ) = m 1 t = 1 ∑ m x i ( t ) x j ( t ) h θ ( x ( t ) ) ( 1 − h θ ( x ( t ) ) )
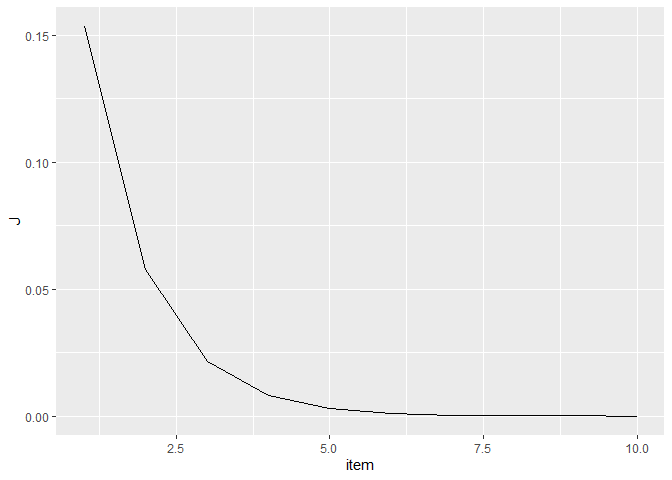
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 HessianMatrix <- function (X, y, theta, num_iters){ m <- length (y) J.history <- rep (0 , num_iters) for (i in 1 :num_iters){ partial1 <- (1 /m) * (t(X) %*% (sigmoid(X %*% theta) - y)) partial2 <- (1 /m) * (t(X) %*% (X * as.numeric ( (sigmoid(X %*% theta) * (1 - sigmoid(X %*% theta))))) ) theta <- theta - solve(partial2) %*% partial1 J.history[i] <- (1 /m) * sum (-y * log (sigmoid(X %*% theta)) - (1 -y) * (log (1 - sigmoid(X %*% theta)))) } return (list (theta = theta, J = J.history)) } X <- as.matrix(wmda[, 2 :3 ]) X <- cbind(1 , X) initial_theta <- matrix(rep (0 , 3 ), ncol = 1 ) Ret <- HessianMatrix(X, y, initial_theta, num_iters = 10 )
## [1] -4.428865 3.158330 12.521196
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 HessianMatrix2 <- function (X, y, theta, num_iters, lambda){ m <- length (y) n <- ncol(X) J.history <- rep (0 , num_iters) for (i in 1 :num_iters){ partial1 <- matrix(rep (0 , n)) partial1[1 ] <- (1 /m) * (t(X[, 1 ]) %*% (sigmoid(X %*% theta) - y)) partial1[2 :n] <- (1 /m) * (t(X[, 2 :n]) %*% (sigmoid(X %*% theta) - y)) + lambda/m * theta[2 :n] partial2 <- (1 /m) * (t(X) %*% (X * as.numeric ( (sigmoid(X %*% theta) * (1 - sigmoid(X %*% theta))))) ) theta <- theta - ginv(partial2) %*% partial1 J.history[i] <- (1 /m) * sum (-y * log (sigmoid(X %*% theta)) - (1 -y) * (log (1 - sigmoid(X %*% theta)))) + (lambda/2 /m) * sum (theta[2 :n] ^2 ) } return (list (theta = theta, J = J.history)) } x1 <- wmda$density x2 <- wmda$sugar X <- mapFeature(x1, x2, 6 ) y <- as.matrix(as.numeric (as.character (wmda$label))) initial_theta <- matrix(rep (0 , 28 ), ncol = 1 ) lambda <- 0 Ret <- HessianMatrix2(X, y, initial_theta, num_iters = 10 , lambda)
## [1] 260.58899 -2305.59070 131.21556 5662.94237 -738.76919 -205.44986
## [7] -2183.57580 2171.56434 -331.49342 268.51504 -5259.69998 -94.64807
## [13] 1782.42515 -318.80433 -889.53148 -933.53588 -2313.77204 1750.42685
## [19] 388.24622 -1015.93544 -1193.47150 6438.19215 -2860.52426 1047.96320
## [25] 531.73182 -599.01104 -1036.47230 -927.34067
## [1] "prediction accuracy = 100 %"
对比可以发现牛顿法比梯度下降法收敛速度快的多!
在最小化代价函数的过程中还有很多更高级的方法,如BFGS(共轭梯度)法、L-BGFS等,它们的优点是不用选择参数α 、收敛速度更快,但是它们也更复杂。
在非线性边界画图中利用的是等值线绘图,也就是将图形分成一个个小的密度点,计算每个密度点的概率值。密度点概率值为0.5的等值线即为边界线。但是在实现过程中geom_isobands()并不能很好实现这个过程。Matlab可以利用函数contour()实现,切记在利用这个函数之前将X 转置。
在HessianMatrix矩阵的求逆过程中并没有利用solve()函数,而是利用了MASS包里的ginv函数,当矩阵不可逆时,这个函数求得矩阵伪逆。类似于Matlab中inv与pinv的关系。
线性判别分析(Linear Discriminant Anaysis,简称LDA)是一种经典的线性学习方法。LDA的思想非常朴素:给定训练集,设法将样本投射到一条直线上,使得同类样本的投影点尽可能接近、异类样本投影点尽可能远离;在对新样本进行分类时,将其投影到同样的直线上,再根据投影点的位置来确定新样本的类型。
将数据点投影到直线θ T \theta^T θ T
y = θ T x y = \theta^Tx
y = θ T x
对于二分类问题,两类样本中心在直线上的投影分别为θ T μ 0 \theta^T \mu_0 θ T μ 0 θ T μ 1 \theta^T \mu_1 θ T μ 1 θ T Σ 0 θ \theta^T \Sigma_0 \theta θ T Σ 0 θ θ T Σ 1 θ \theta^T \Sigma_1 \theta θ T Σ 1 θ
∑ x ∈ D i ( θ T x − θ T μ i ) 2 = ∑ x ∈ D i ( θ T ( x − μ i ) ) 2 = ∑ x ∈ D i θ T ( x − μ i ) ( x − μ i ) T θ = θ T ∑ x ∈ D i [ ( x − μ i ) ( x − μ i ) T ] θ = θ T Σ i θ \begin{aligned}
\sum_{x \in D_{i}}\left(\theta^{T} x-\theta^{T} \mu_{i}\right)^{2} &=\sum_{x \in D_{i}}\left(\theta^{T}\left(x-\mu_{i}\right)\right)^{2} \\
&=\sum_{x \in D_{i}} \theta^{T}\left(x-\mu_{i}\right)\left(x-\mu_{i}\right)^{T} \theta \\
&=\theta^{T} \sum_{x \in D_{i}}\left[\left(x-\mu_{i}\right)\left(x-\mu_{i}\right)^{T}\right] \theta \\
&=\theta^{T} \Sigma_{i} \theta
\end{aligned}
x ∈ D i ∑ ( θ T x − θ T μ i ) 2 = x ∈ D i ∑ ( θ T ( x − μ i ) ) 2 = x ∈ D i ∑ θ T ( x − μ i ) ( x − μ i ) T θ = θ T x ∈ D i ∑ [ ( x − μ i ) ( x − μ i ) T ] θ = θ T Σ i θ
欲使同类样本的投影点尽可能接近,可以让同类样本的协方差尽可能的小(类似于方差代表样本离散程度),即θ T Σ 0 θ + θ T Σ 1 θ \theta^T \Sigma_0 \theta + \theta^T \Sigma_1 \theta θ T Σ 0 θ + θ T Σ 1 θ ∣ ∣ θ T μ 0 − θ T μ 1 ∣ ∣ 2 2 ||\theta^T\mu_0 - \theta^T\mu_1||_2^2 ∣ ∣ θ T μ 0 − θ T μ 1 ∣ ∣ 2 2
J = ∥ θ T μ 0 − θ T μ 1 ∥ 2 2 θ T Σ 0 θ + θ T Σ 1 θ = θ T ( μ 0 − μ 1 ) ( μ 0 − μ 1 ) T θ θ T ( Σ 0 + Σ 1 ) θ \begin{aligned}
J &=\frac{\left\|\theta^{T} \mu_{0}-\theta^{T} \mu_{1}\right\|_{2}^{2}}{\theta^{T} \Sigma_{0} \theta+\theta^{T} \Sigma_{1} \theta} \\
&=\frac{\theta^{T}\left(\mu_{0}-\mu_{1}\right)\left(\mu_{0}-\mu_{1}\right)^{T} \theta}{\theta^{T}\left(\Sigma_{0}+\Sigma_{1}\right) \theta}
\end{aligned}
J = θ T Σ 0 θ + θ T Σ 1 θ ∥ ∥ θ T μ 0 − θ T μ 1 ∥ ∥ 2 2 = θ T ( Σ 0 + Σ 1 ) θ θ T ( μ 0 − μ 1 ) ( μ 0 − μ 1 ) T θ
定义类内散度矩阵(within-class scatter matrix):
S w = Σ 0 + Σ 1 = ∑ x ∈ D 0 ( x − μ 0 ) ( x − μ 0 ) T + ∑ x ∈ D 1 ( x − μ 1 ) ( x − μ 1 ) T \begin{aligned}
S_{w} &=\Sigma_{0}+\Sigma_{1} \\
&=\sum_{x \in D_{0}}\left(x-\mu_{0}\right)\left(x-\mu_{0}\right)^{T}+\sum_{x \in D_{1}}\left(x-\mu_{1}\right)\left(x-\mu_{1}\right)^{T}
\end{aligned}
S w = Σ 0 + Σ 1 = x ∈ D 0 ∑ ( x − μ 0 ) ( x − μ 0 ) T + x ∈ D 1 ∑ ( x − μ 1 ) ( x − μ 1 ) T
定义类间散度矩阵(between-class scatter matrix):
S b = ( μ 0 − μ 1 ) ( μ 0 − μ 1 ) T S_b = (\mu_0 - \mu_1)(\mu_0 - \mu_1)^T
S b = ( μ 0 − μ 1 ) ( μ 0 − μ 1 ) T
则:
J = θ T S b θ θ T S w θ J = \dfrac{\theta^TS_b\theta}{\theta^T S_w \theta }
J = θ T S w θ θ T S b θ
我们优化的目标就是使J J J θ \theta θ θ \theta θ θ T S w θ = 1 \theta^T S_w \theta = 1 θ T S w θ = 1
min θ − θ T S b θ \min_\theta -\theta^TS_b\theta
θ min − θ T S b θ
s . t . θ T S w θ = 1 s.t.\theta^T S_w \theta = 1
s . t . θ T S w θ = 1
利用拉格朗日乘子法化解上式可得:
c ( θ ) = θ T S b θ − λ ( θ T S w θ − 1 ) c(\theta) = \theta^TS_b\theta - \lambda(\theta^T S_w \theta - 1)
c ( θ ) = θ T S b θ − λ ( θ T S w θ − 1 )
d c d θ = 2 S b θ − 2 λ S w θ = 0 \dfrac{dc}{d\theta} = 2S_b\theta - 2\lambda S_w\theta = 0
d θ d c = 2 S b θ − 2 λ S w θ = 0
S w − 1 S b θ = λ θ S_w^{-1}S_b\theta = \lambda\theta
S w − 1 S b θ = λ θ
参数θ \theta θ S w − 1 S b S_w^{-1}S_b S w − 1 S b S b θ S_b\theta S b θ μ 0 − μ 1 \mu_0-\mu_1 μ 0 − μ 1 S b θ = λ ( μ 0 − μ 1 ) S_b\theta = \lambda(\mu_0 - \mu_1) S b θ = λ ( μ 0 − μ 1 )
S b θ = ( μ 0 − μ 1 ) ( μ 0 − μ 1 ) T θ S_b\theta = (\mu_0 - \mu_1)(\mu_0 - \mu_1)^T \theta
S b θ = ( μ 0 − μ 1 ) ( μ 0 − μ 1 ) T θ
其中( μ 0 − μ 1 ) T θ (\mu_0 - \mu_1)^T \theta ( μ 0 − μ 1 ) T θ
最终化简结果为:
θ = S w − 1 ( μ 0 − μ 1 ) \theta = S_w^{-1}(\mu_0 - \mu_1)
θ = S w − 1 ( μ 0 − μ 1 )
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 LDA <- function (X, y){ pos <- which(y == 1 ) neg <- which(y == 0 ) u1 <- as.matrix(colMeans(X[pos, ])) u0 <- as.matrix(colMeans(X[neg, ])) Sw <- (t(X[pos, ]) - as.numeric (u1)) %*% t(t(X[pos, ]) - as.numeric (u1)) + (t(X[neg, ]) - as.numeric (u0)) %*% t(t(X[neg, ]) - as.numeric (u0)) theta <- ginv(Sw) %*% (u0 - u1) return (list (u1=u1, u0=u0, theta = theta)) } X <- as.matrix(wmda[, 2 :3 ]) y <- as.matrix(as.numeric (as.character (wmda$label))) Ret <- LDA(X, y) theta <- Ret$theta print(theta)
## [,1]
## [1,] -0.1465098
## [2,] -0.7387156
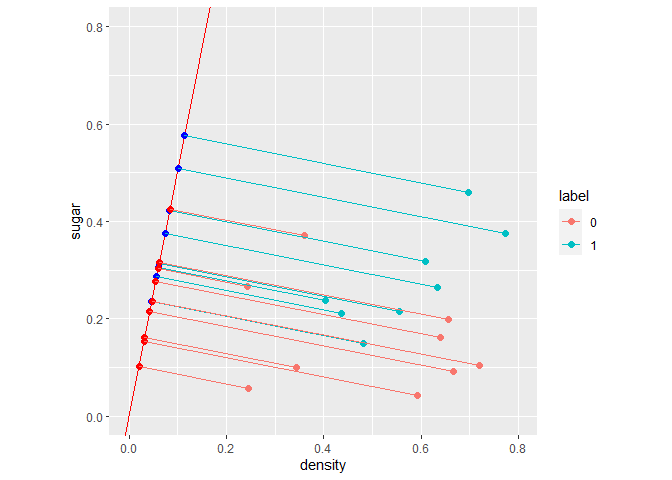
θ T \theta^T θ T theta[2]/theta[1],截距为0 0 0 θ T \theta^T θ T θ T \theta^T θ T θ T \theta^T θ T
设k = θ 2 / θ 1 k=\theta_2/\theta_1 k = θ 2 / θ 1 θ T \theta^T θ T θ T \theta^T θ T y = k x y=kx y = k x − 1 / k -1/k − 1 / k y = k x y=kx y = k x
{ y = k x y − y i = − 1 / k ( x − x i ) \begin{cases}
y=kx \\
y-y_i = -1/k(x-x_i)
\end{cases}
{ y = k x y − y i = − 1 / k ( x − x i )
解得
x = 1 k x i + y i 1 k + 1 ; y = x i + k y i 1 k + 1 x= \dfrac{\dfrac{1}{k}x_i + y_i}{\dfrac{1}{k} + 1};
y= \dfrac{x_i + ky_i}{\dfrac{1}{k} + 1}
x = k 1 + 1 k 1 x i + y i ; y = k 1 + 1 x i + k y i
在本节开始中有提到对新样本进行分类时,将其投影到同样的这条直线上,再根据投影点的位置来判断新样本的类别。在这里我们取决策边界为θ T μ 0 \theta^T\mu_0 θ T μ 0 θ T μ 1 \theta^T\mu_1 θ T μ 1 − 1 / k -1/k − 1 / k 1 k x 1 + y 1 \dfrac{1}{k}x_1 + y_1 k 1 x 1 + y 1
假设存在N N N i i i m i m_i m i
S t = S b + S w = ∑ i = 1 m ( x i − μ ) ( x i − μ ) T \begin{aligned}
S_{t} &=S_{b}+S_{w} \\
&=\sum_{i=1}^{m}\left(x_{i}-\mu\right)\left(x_{i}-\mu\right)^{T}
\end{aligned}
S t = S b + S w = i = 1 ∑ m ( x i − μ ) ( x i − μ ) T
其中μ \mu μ S w S_w S w
S w = ∑ i = 1 N ∑ x ∈ D i ( x − μ i ) ( x − μ i ) T S_w = \sum_{i=1}^N \sum_{x\in D_i}(x-\mu_i)(x-\mu_i)^T
S w = i = 1 ∑ N x ∈ D i ∑ ( x − μ i ) ( x − μ i ) T
则S b S_b S b
S b = S t − S w = ∑ i = 1 N m i ( μ i − μ ) ( μ i − μ ) T \begin{aligned}
S_{b} &=S_{t}-S_{w} \\
&=\sum_{i=1}^{N} m_{i}\left(\mu_{i}-\mu\right)\left(\mu_{i}-\mu\right)^{T}
\end{aligned}
S b = S t − S w = i = 1 ∑ N m i ( μ i − μ ) ( μ i − μ ) T
通过求广义特征值方法求解θ \theta θ
S w − 1 S b θ = λ θ S_w^{-1}S_b\theta = \lambda\theta
S w − 1 S b θ = λ θ
θ \theta θ S w − 1 S b S_w^{-1}S_b S w − 1 S b
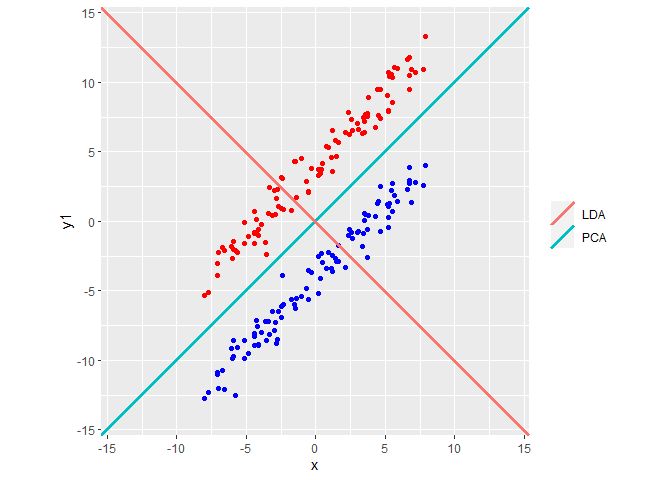
LDA是一种经典的监督式降维技术。PCA是一种无监督的数据降维方法。我们知道即使在训练样本上,我们提供了类别标签,在使用PCA模型的时候,我们是不利用类别标签的,而LDA在进行数据降维的时候是利用数据的类别标签提供的信息的。
从几何的角度来看,PCA和LDA都是将数据投影到新的相互正交的坐标轴上。只不过在投影的过程中他们使用的约束是不同的,也可以说目标是不同的。PCA是将数据投影到方差最大的几个相互正交的方向上,以期待保留最多的样本信息。样本的方差越大表示样本的多样性越好,在训练模型的时候,我们当然希望数据的差别越大越好。否则即使样本很多但是他们彼此相似或者相同,提供的样本信息将相同,相当于只有很少的样本提供信息是有用的。但是,对于一些特殊分布的数据集,PCA的这个投影后方差最大的目标就不太合适了。比如下图:
奇异值分解(Singular Value Decomposition, 简称SVD)是在机器学习领域广泛应用的算法,它不光可以用于降维算法中的特征分解,还可以用于推荐系统,以及自然语言处理等领域。
SVD是对矩阵进行分解。假设我们的矩阵A是一个m × n m\times n m × n
A = U Σ V T A = U\Sigma V^T
A = U Σ V T
其中U是一个m × m m\times m m × m Σ \Sigma Σ m × n m\times n m × n n × n n\times n n × n U T U = I U^TU = I U T U = I V T V = I V^TV=I V T V = I
如果我们将A的转置和A做矩阵乘法,对A T A A^TA A T A m × n m\times n m × n
( A T A ) v i = λ i v i (A^TA)v_i = \lambda_iv_i
( A T A ) v i = λ i v i
这样我们就可以得到矩阵A T A A^TA A T A v v v
将A T A A^TA A T A n × n n\times n n × n
同样我们将A和A的转置做矩阵乘法,会得到一个m × m m\times m m × m A A T AA^T A A T m × m m\times m m × m
A = U Σ V T ⇒ A T = V Σ T U T ⇒ A T A = V Σ 2 V T A = U\Sigma V^T \Rightarrow A^T = V\Sigma^TU^T \Rightarrow A^TA = V\Sigma^2V^T
A = U Σ V T ⇒ A T = V Σ T U T ⇒ A T A = V Σ 2 V T
从上式我们可以看出A T A A^TA A T A A T A A^TA A T A
σ i = λ i \sigma_i = \sqrt{\lambda_i}
σ i = √ λ i
举例:
A = [ 0 1 1 1 1 0 ] A=
\begin{bmatrix}
0 & 1 \\
1 & 1 \\
1 & 0 \\
\end{bmatrix}
A = ⎣ ⎢ ⎢ ⎡ 0 1 1 1 1 0 ⎦ ⎥ ⎥ ⎤
求得
A T A = [ 2 1 1 2 ] A^TA=
\begin{bmatrix}
2 & 1 \\
1 & 2 \\
\end{bmatrix}
A T A = ⎣ ⎡ 2 1 1 2 ⎦ ⎤
A A T = [ 1 1 0 1 2 1 0 1 1 ] AA^T=
\begin{bmatrix}
1 & 1 & 0\\
1 & 2 & 1\\
0 & 1 & 1\\
\end{bmatrix}
A A T = ⎣ ⎢ ⎢ ⎡ 1 1 0 1 2 1 0 1 1 ⎦ ⎥ ⎥ ⎤
进而求得A T A A^TA A T A
λ 1 = 3 ; v 1 = ( 1 2 ; 1 2 ) ; λ 2 = 1 ; v 2 = ( − 1 2 ; 1 2 ) \lambda_1=3;v_1 = (\frac{1}{\sqrt{2}};\frac{1}{\sqrt{2}});
\lambda_2=1;v_2 = (-\frac{1}{\sqrt{2}};\frac{1}{\sqrt{2}})
λ 1 = 3 ; v 1 = ( √ 2 1 ; √ 2 1 ) ; λ 2 = 1 ; v 2 = ( − √ 2 1 ; √ 2 1 )
A A T AA^T A A T
λ 1 = 3 ; u 1 = ( 1 6 ; 2 6 ; 1 6 ) ; λ 2 = 1 ; u 2 = ( 1 2 ; 0 ; − 1 2 ) ; λ 3 = 0 ; u 3 = ( 1 3 ; − 1 3 ; 1 3 ) \lambda_1=3;u_1 = (\frac{1}{\sqrt{6}};\frac{2}{\sqrt{6}};\frac{1}{\sqrt{6}});
\lambda_2=1;u_2 = (\frac{1}{\sqrt{2}};0;-\frac{1}{\sqrt{2}});
\lambda_3=0;u_3 = (\frac{1}{\sqrt{3}};-\frac{1}{\sqrt{3}};\frac{1}{\sqrt{3}})
λ 1 = 3 ; u 1 = ( √ 6 1 ; √ 6 2 ; √ 6 1 ) ; λ 2 = 1 ; u 2 = ( √ 2 1 ; 0 ; − √ 2 1 ) ; λ 3 = 0 ; u 3 = ( √ 3 1 ; − √ 3 1 ; √ 3 1 )
利用σ i = λ i \sigma_i = \sqrt{\lambda_i} σ i = √ λ i σ 1 = 3 , σ 2 = 1 \sigma_1 = \sqrt{3},\sigma_2 = 1 σ 1 = √ 3 , σ 2 = 1
最终A的奇异值分解为:
A = U Σ V T = [ 1 6 1 2 1 3 2 6 0 − 1 3 1 6 − 1 2 1 3 ] [ 3 0 0 1 0 0 ] [ 1 2 1 2 − 1 2 1 2 ] A = U \Sigma V^T =
\begin{bmatrix}
\frac{1}{\sqrt{6}} & \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{3}}\\
\frac{2}{\sqrt{6}} & 0 & -\frac{1}{\sqrt{3}}\\
\frac{1}{\sqrt{6}} & -\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{3}}\\
\end{bmatrix}
\begin{bmatrix}
\sqrt{3} & 0 \\
0 & 1 \\
0 & 0 \\
\end{bmatrix}
\begin{bmatrix}
\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\
-\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\
\end{bmatrix}
A = U Σ V T = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ √ 6 1 √ 6 2 √ 6 1 √ 2 1 0 − √ 2 1 √ 3 1 − √ 3 1 √ 3 1 ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ ⎣ ⎢ ⎢ ⎡ √ 3 0 0 0 1 0 ⎦ ⎥ ⎥ ⎤ ⎣ ⎢ ⎢ ⎢ ⎡ √ 2 1 − √ 2 1 √ 2 1 √ 2 1 ⎦ ⎥ ⎥ ⎥ ⎤
备注:eigen()可以用来计算特征值与特征向量。
对于奇异值,它跟我们特征分解中的特征值类似,在奇异值矩阵中也是按照从大到小排列,而且奇异值的减少特别的快,在很多情况下,前10%甚至1%的奇异值的和就占了全部的奇异值之和的99%以上的比例。也就是说,我们也可以用最大的k个的奇异值和对应的左右奇异向量来近似描述矩阵。
从csv文件中读取西瓜数据,并进行展示。
1 2 wmda <- read.csv(file = "Test3/西瓜数据2.0.csv" ) wmda[, 8 ] <- as.factor(wmda[, 8 ])
编号
色泽
根蒂
敲声
纹理
脐部
触感
label
1
青绿
蜷缩
浊响
清晰
凹陷
硬滑
1
2
乌黑
蜷缩
沉闷
清晰
凹陷
硬滑
1
3
乌黑
蜷缩
浊响
清晰
凹陷
硬滑
1
4
青绿
蜷缩
沉闷
清晰
凹陷
硬滑
1
5
浅白
蜷缩
浊响
清晰
凹陷
硬滑
1
6
青绿
稍蜷
浊响
清晰
稍凹
软粘
1
7
乌黑
稍蜷
浊响
稍糊
稍凹
软粘
1
8
乌黑
稍蜷
浊响
清晰
稍凹
硬滑
1
9
乌黑
稍蜷
沉闷
稍糊
稍凹
硬滑
0
10
青绿
硬挺
清脆
清晰
平坦
软粘
0
11
浅白
硬挺
清脆
模糊
平坦
硬滑
0
12
浅白
蜷缩
浊响
模糊
平坦
软粘
0
13
青绿
稍蜷
浊响
稍糊
凹陷
硬滑
0
14
浅白
稍蜷
沉闷
稍糊
凹陷
硬滑
0
15
乌黑
稍蜷
浊响
清晰
稍凹
软粘
0
16
浅白
蜷缩
浊响
模糊
平坦
硬滑
0
17
青绿
蜷缩
沉闷
稍糊
稍凹
硬滑
0
决策树(decision tree)是一种基本的分类与回归方法。这里主要讨论分类树。决策树模型呈树形结构,在分类问题中,表示基于特征对实例进行分类的过程。它可以认为是if-then规则的集合,也可以认为是定义在特征空间与类空间上的条件概率分布。其主要优点是模型具有可读性,分类速度快。学习时,利用训练数据,根据损失函数最小化的原则建立决策树模型。预测时,对新的数据,利用决策树模型进行分类。
决策树学习通常包括3个步骤:特征选择、决策树的生成和决策树的修剪。这些决策树学习的思想主要来源于Quinlan在1986年提出的ID3算法和1993年提出的C4.5算法,以及由Breiman等人在1984年提出的CART算法。
“信息熵”(information entropy)是度量样本集合纯度常用的一种指标。假定当前样本集合D D D k k k p k ( k = 1 , 2 , … , y ) p_k(k=1,2,\ldots, y) p k ( k = 1 , 2 , … , y ) D D D
E n t ( D ) = − ∑ i = 1 y p k l o g 2 p k Ent(D)=-\sum_{i=1}^yp_klog_2p_k
E n t ( D ) = − i = 1 ∑ y p k l o g 2 p k
E n t ( D ) Ent(D) E n t ( D ) D D D
信息增益是指离散属性a a a D D D
G a i n ( D , a ) = E n t ( D ) − ∑ v = 1 V D v D E n t ( D v ) Gain(D,a)=Ent(D)-\sum_{v=1}^V \frac{D^v}{D}Ent(D^v)
G a i n ( D , a ) = E n t ( D ) − v = 1 ∑ V D D v E n t ( D v )
其中V V V a a a V V V D v D \frac{D^v}{D} D D v a a a
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 TreeGenerate <- function (da, method = "ID3" ){ CalEnt <- function (pk){ Entd <- -(pk * log2(pk)) Entd[is.na (Entd)] <- 0 Entd <- sum (Entd) return (Entd) } tree <- list () pvec <- as.numeric (table(da[, ncol(da)])) / nrow(da) Entd <- CalEnt(pvec) tree[[1 ]] <- list (a = "boot" , aname = "boot" , boot = da[, 1 ], Entd = Entd) a <- 2 dalist <- list (da = list (da = da), count = 1 ) treelast <- list () treenew <- list () while (length (dalist$da) > 0 ){ Retlist <- list () k <- 1 dalistnew <- list () for (t in 1 :length (dalist$da)){ count <- dalist$count dat <- dalist$da[[t]] pvec <- as.numeric (table(dat[, ncol(dat)])) / nrow(dat) Entd <- CalEnt(pvec) AEnt <- rep (0 , length = ncol(dat) - 2 ) IV <- AEnt Gini <- rep (0 , length = ncol(dat) - 2 ) ARetlist <- list () for (i in 2 :(ncol(dat)-1 )){ avec <- levels(as.factor(dat[, i])) aretlist <- list () for (j in 1 :length (avec)){ aj.boot <- dat[which(dat[, i] == avec[j]), 1 ] pvec <- table(dat[which(dat[, 1 ] %in% aj.boot), ncol(dat)]) pvec <- as.numeric (pvec) / length (aj.boot) AEnt[i-1 ] <- AEnt[i-1 ] + CalEnt(pvec) * length (aj.boot) / nrow(dat) IV[i-1 ] <- IV[i-1 ] - length (aj.boot) / nrow(dat) * log2(length (aj.boot) / nrow(dat)) Gini[i-1 ] <- Gini[i-1 ] + (1 -sum (pvec^2 )) * length (aj.boot) / nrow(dat) aretlist[[j]] <- list (a = colnames(dat)[i], aname = avec[j], boot = aj.boot, Entd = CalEnt(pvec)) } ARetlist[[i-1 ]] <- aretlist } if (method == "ID3" ){ ret <- ARetlist[[which(AEnt == min (AEnt))[1 ]]] } if (method == "C4.5" ){ ind <- which(AEnt <= mean(AEnt)) Gr <- (1 - AEnt[ind]) / IV[ind] ret <- ARetlist[[ind[which(Gr == max (Gr))[1 ]]]] } if (method == "Gini" ){ ret <- ARetlist[[which(Gini == min (Gini))[1 ]]] } retlist <- list () if (count == 1 ){ print(paste("||" , "Boot" , " {" , paste(da[, 1 ], collapse = "," ) ,"} " , "Ent = " , round (tree[[1 ]]$Entd, 3 ), sep = "" )) }else { print(paste(paste(rep (".." , count-1 ), collapse = "." ), count-1 , ")" , tail(treelast[[t]]$a, 1 ), "=" , tail(treelast[[t]]$aname, 1 ), " {" , paste(treelast[[t]]$boot, collapse = "," ) ,"} " , sep = "" )) } for (i in 1 : length (ret)){ if (count == 1 ){ treelast <- tree } classe <- as.character (da[which(da[, 1 ] %in% ret[[i]]$boot), ncol(da)]) classe <- table(as.numeric (classe)) if (ret[[i]]$Entd == 0 | length (ret[[i]]$boot) == 0 ){ print(paste(paste(rep (".." , count), collapse = "." ), count, ")" , ret[[i]]$a, "=" , ret[[i]]$aname, " {" , paste(ret[[i]]$boot, collapse = "," ), "} " , ifelse(names (which(classe == max (classe)))[1 ] == 1 , "Good" , "Bad" ), sep = "" )) retlist[[i]] <- list (a = c (treelast[[t]]$a, ret[[i]]$a), aname = c (treelast[[t]]$aname, ret[[i]]$aname), boot = ret[[i]]$boot, Entd = ret[[i]]$Entd, class = names (which(classe == max (classe)))[1 ]) } if (ret[[i]]$Entd != 0 & length (ret[[i]]$boot) != 0 ){ dalistnew[[k]] <- dat[which(dat[, 1 ] %in% ret[[i]]$boot), -which(colnames(dat) == ret[[i]]$a)] treenew[[k]] <- list (a = c (treelast[[t]]$a, ret[[i]]$a), aname = c (treelast[[t]]$aname, ret[[i]]$aname), boot = ret[[i]]$boot, Entd = ret[[i]]$Entd, class = names (which(classe == max (classe)))[1 ]) k <- k + 1 } } Retlist[[t]] <- retlist } count <- count + 1 tree[[count]] <- Retlist dalistnew <- list (da = dalistnew, count = count) dalist <- dalistnew treelast <- treenew } return (tree) } Tree <- TreeGenerate(wmda, method = "ID3" )
## [1] "||Boot {1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17} Ent = 0.998"
## [1] "..1)纹理=模糊 {11,12,16} Bad"
## [1] "..1)纹理=清晰 {1,2,3,4,5,6,8,10,15} "
## [1] ".....2)根蒂=蜷缩 {1,2,3,4,5} Good"
## [1] ".....2)根蒂=硬挺 {10} Bad"
## [1] "..1)纹理=稍糊 {7,9,13,14,17} "
## [1] ".....2)触感=软粘 {7} Good"
## [1] ".....2)触感=硬滑 {9,13,14,17} Bad"
## [1] ".....2)根蒂=稍蜷 {6,8,15} "
## [1] "........3)色泽=青绿 {6} Good"
## [1] "........3)色泽=乌黑 {8,15} "
## [1] "...........4)触感=软粘 {15} Bad"
## [1] "...........4)触感=硬滑 {8} Good"
信息增益准则对可取值数目较多的属性有所偏好,为减少这种偏好可能带来的不利影响,Quinlan在1993年提出了C4.5算法,使用“增益率”(gain ratio)来选择最优划分属性。增益率的定义为:
G a i n _ r a t i o ( D , a ) = G a i n ( D , a ) I V ( a ) Gain\_ratio(D, a) = \dfrac{Gain(D, a)}{IV(a)}
G a i n _ r a t i o ( D , a ) = I V ( a ) G a i n ( D , a )
其中
I V ( a ) = − ∑ v = 1 V D v D l o g 2 D v D IV(a) = -\sum_{v=1}^V \frac{D^v}{D}log_2 \frac{D^v}{D}
I V ( a ) = − v = 1 ∑ V D D v l o g 2 D D v
属性a a a I V ( a ) IV(a) I V ( a )
生成树TreeGenerate()函数中已经包含C4.5算法,仅需将method参数改为“C4.5”即可。
1 Tree <- TreeGenerate(wmda, method = "C4.5" )
## [1] "||Boot {1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17} Ent = 0.998"
## [1] "..1)纹理=模糊 {11,12,16} Bad"
## [1] "..1)纹理=清晰 {1,2,3,4,5,6,8,10,15} "
## [1] ".....2)触感=硬滑 {1,2,3,4,5,8} Good"
## [1] "..1)纹理=稍糊 {7,9,13,14,17} "
## [1] ".....2)触感=软粘 {7} Good"
## [1] ".....2)触感=硬滑 {9,13,14,17} Bad"
## [1] ".....2)触感=软粘 {6,10,15} "
## [1] "........3)色泽=乌黑 {15} Bad"
## [1] "........3)色泽=青绿 {6,10} "
## [1] "...........4)根蒂=稍蜷 {6} Good"
## [1] "...........4)根蒂=硬挺 {10} Bad"
CART决策树[Breimaan et al. 1984]使用“基尼系数”(Gini index)来选择划分属性。数据集D的纯度可以用基尼值来度量:
Gini(D)=\sum_{k=1}^y \sum_{k'\not=k}p_kp_{k'} = 1-\sum_{k=1}^yp_k^2
基尼系数越小则数据集的纯度越高。属性a a a
G i n i i n d e x ( D , a ) = ∑ v = 1 V D v D G i n i ( D v ) Gini_index(D, a) = \sum_{v=1}^V \frac{D^v}{D}Gini(D^v)
G i n i i n d e x ( D , a ) = v = 1 ∑ V D D v G i n i ( D v )
1 Tree <- TreeGenerate(wmda, method = "Gini" )
## [1] "||Boot {1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17} Ent = 0.998"
## [1] "..1)纹理=模糊 {11,12,16} Bad"
## [1] "..1)纹理=清晰 {1,2,3,4,5,6,8,10,15} "
## [1] ".....2)根蒂=蜷缩 {1,2,3,4,5} Good"
## [1] ".....2)根蒂=硬挺 {10} Bad"
## [1] "..1)纹理=稍糊 {7,9,13,14,17} "
## [1] ".....2)触感=软粘 {7} Good"
## [1] ".....2)触感=硬滑 {9,13,14,17} Bad"
## [1] ".....2)根蒂=稍蜷 {6,8,15} "
## [1] "........3)色泽=青绿 {6} Good"
## [1] "........3)色泽=乌黑 {8,15} "
## [1] "...........4)触感=软粘 {15} Bad"
## [1] "...........4)触感=硬滑 {8} Good"
通过对比发现,ID3与CART算法得到了相同得决策树。C4.5算法得到的决策树在第二层中选择了较少类别的属性(触感)。
决策树剪枝的基本策略有“预剪枝”(prepruning)和“后剪枝”(postpruning)[Quinlan,1993]。
预剪枝是指在决策树生成过程中,对每个结点在划分前先进行估计,若当前节点的划分不能带来决策树泛化能力提升,则停止划分并将当前结点标记为叶节点。(需要划分训练集与测试集,根据准确率进行性能评估)
首先划分训练集与测试集:
1 2 wmda.train <- wmda[c (1 ,2 ,3 ,6 ,7 ,10 ,14 :17 ), c (1 ,6 ,2 ,3 ,4 ,5 ,7 ,8 )] wmda.test <- wmda[c (4 ,5 ,8 ,9 ,11 :13 ), c (1 ,6 ,2 ,3 ,4 ,5 ,7 ,8 )]
没有预剪枝的决策树为:
1 Tree.train <- TreeGenerate(wmda.train, method = "ID3" )
## [1] "||Boot {1,2,3,6,7,10,14,15,16,17} Ent = 1"
## [1] "..1)脐部=平坦 {10,16} Bad"
## [1] "..1)脐部=凹陷 {1,2,3,14} "
## [1] ".....2)色泽=浅白 {14} Bad"
## [1] ".....2)色泽=青绿 {1} Good"
## [1] ".....2)色泽=乌黑 {2,3} Good"
## [1] "..1)脐部=稍凹 {6,7,15,17} "
## [1] ".....2)根蒂=蜷缩 {17} Bad"
## [1] ".....2)根蒂=稍蜷 {6,7,15} "
## [1] "........3)色泽=青绿 {6} Good"
## [1] "........3)色泽=乌黑 {7,15} "
## [1] "...........4)纹理=清晰 {15} Bad"
## [1] "...........4)纹理=稍糊 {7} Good"
剪枝后的树为:
1 Tree <- TreeGenerate2(wmda.train, wmda.test, method = "ID3" )
## [1] "||Boot {1,2,3,6,7,10,14,15,16,17} Ent = 1"
## [1] "..1)脐部=平坦 {10,16} Bad"
## [1] "..1)脐部=凹陷 {1,2,3,14} "
## [1] "Class:Good"
## [1] "No increase in accuracy, terminate classification"
## [1] "..1)脐部=稍凹 {6,7,15,17} "
## [1] "Class:Bad"
## [1] "No increase in accuracy, terminate classification"
先生成整棵树,通过判断剪枝后的精度是否提高进行剪枝处理。后剪枝决策树通常比预剪枝决策树保留了更多的分支,一般情况下,后剪枝决策树的欠拟合风险很小,泛化性能往往优于预剪枝决策树。
C4.5算法中采用二分法(bi-partition)对连续属性进行处理。给定样本集D D D a a a a a a D D D n n n
T a = { a i + a i + 1 2 ∣ 1 ⩽ i ⩽ n − 1 } T_a = \{\frac{a^i + a^{i+1}}{2} |1\leqslant i \leqslant n-1 \}
T a = { 2 a i + a i + 1 ∣ 1 ⩽ i ⩽ n − 1 }
1 2 3 wmda <- read.csv(file = "Test3/西瓜数据3.0.csv" ) wmda[, 10 ] <- as.factor(wmda[, 10 ]) knitr::kable(head(wmda, 2 ))
编号
色泽
根蒂
敲声
纹理
脐部
触感
密度
含糖率
label
1
青绿
蜷缩
浊响
清晰
凹陷
硬滑
0.697
0.460
1
2
乌黑
蜷缩
沉闷
清晰
凹陷
硬滑
0.774
0.376
1
1 Tree <- TreeGenerate3(wmda)
## [1] "||Boot {1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17} Ent = 0.998"
## [1] "..1)纹理=模糊 {11,12,16} Bad"
## [1] "..1)纹理=清晰 {1,2,3,4,5,6,8,10,15} "
## [1] ".....2)密度=<= 0.3815 {10,15} Bad"
## [1] ".....2)密度=> 0.3815 {1,2,3,4,5,6,8} Good"
## [1] "..1)纹理=稍糊 {7,9,13,14,17} "
## [1] ".....2)触感=软粘 {7} Good"
## [1] ".....2)触感=硬滑 {9,13,14,17} Bad"
多变量决策树把每个属性视为坐标空间中的一个坐标轴,则d d d d d d
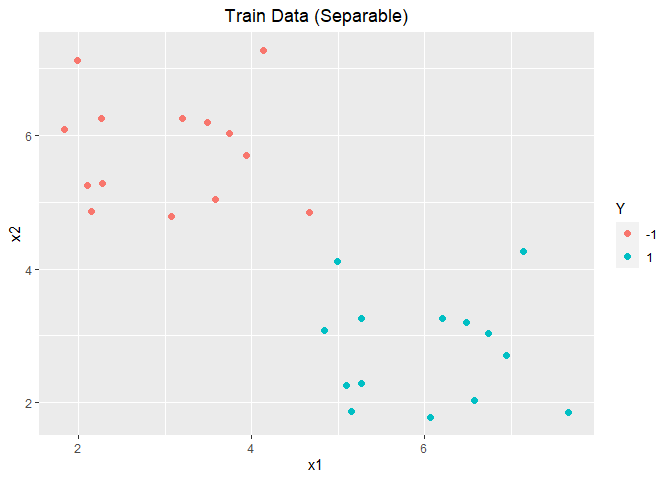
随机生成服从二元正态分布的40个样本,其中20个样本均值为[ 3 , 6 ] T [3,6]^T [ 3 , 6 ] T [ 6 , 3 ] T [6,3]^T [ 6 , 3 ] T
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 CreatData <- function (n, mu1, mu2, Sigma, seed = 3 , alha = 0.7 ){ set.seed(seed) X1 <- mvrnorm(n, mu1, Sigma) X1 <- data.frame(x1 = X1[, 1 ], x2 = X1[, 2 ]) Y1 <- rep (-1 , n) set.seed(seed) X2 <- mvrnorm(n, mu2, Sigma) X2 <- data.frame(x1 = X2[, 1 ], x2 = X2[, 2 ]) Y2 <- rep (1 , n) X1.train <- X1[1 :floor (n*alha), ] X1.test <- X1[(floor (n*alha) + 1 ):n, ] X2.train <- X2[1 :floor (n*alha), ] X2.test <- X2[(floor (n*alha) + 1 ):n, ] Y1.train <- Y1[1 :floor (n*alha)] Y1.test <- Y1[(floor (n*alha) + 1 ):n] Y2.train <- Y2[1 :floor (n*alha)] Y2.test <- Y2[(floor (n*alha) + 1 ):n] X.train <- rbind(X1.train, X2.train) X.test <- rbind(X1.test, X2.test) Y.train <- data.frame(Y = as.factor(c (Y1.train, Y2.train))) Y.test <- data.frame(Y = as.factor(c (Y1.test, Y2.test))) return (list (data.train = cbind(X.train, Y.train), data.test = cbind(X.test, Y.test))) } data1 <- CreatData(20 , c (3 , 6 ), c (6 , 3 ), diag(2 )) data1.train <- data1$data.train data1.test <- data1$data.test ggplot(data = data1.train, aes(x = x1, y = x2, colour = Y)) + geom_point(size = 2.0 , shape = 16 ) + labs(title="Train Data (Separable)" ) + theme(plot.title = element_text(hjust = 0.5 ))
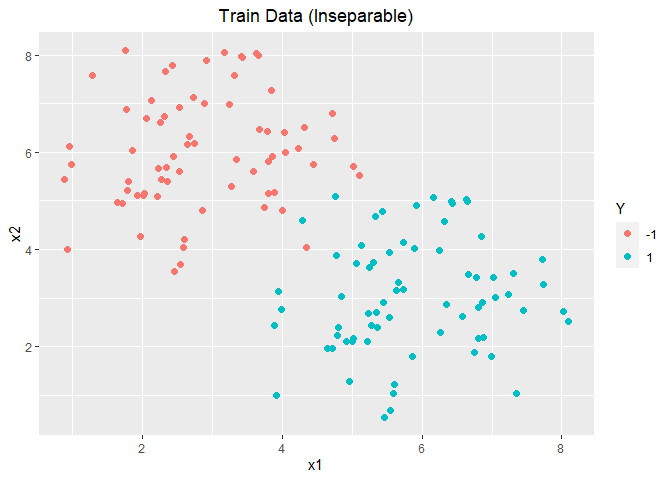
随机生成服从二元正态分布的200个样本,其中100个样本均值为[ 3 , 6 ] T [3,6]^T [ 3 , 6 ] T [ 6 , 3 ] T [6,3]^T [ 6 , 3 ] T
1 2 3 4 5 6 data2 <- CreatData(100 , c (3 , 6 ), c (6 , 3 ), diag(2 ), seed = 2 ) data2.train <- data2$data.train data2.test <- data2$data.test ggplot(data = data2.train, aes(x = x1, y = x2, colour = Y)) + geom_point(size = 2.0 , shape = 16 ) + labs(title="Train Data (Inseparable)" ) + theme(plot.title = element_text(hjust = 0.5 ))
支持向量机就是找最优超平面去划分样本。超平面可以通过线性方程w T + b = 0 w^T + b = 0 w T + b = 0 w = ( w 1 ; w 2 ; . . . ; w d ) w=(w_1;w_2;...;w_d) w = ( w 1 ; w 2 ; . . . ; w d ) b b b
样本空间中任意一点x x x ( w , b ) (w, b) ( w , b )
r = ∣ w T x + b ∣ ∣ ∣ w ∣ ∣ r = \frac{|w^Tx+b|}{||w||}
r = ∣ ∣ w ∣ ∣ ∣ w T x + b ∣
最优的超平面就是使得距离超平面最近的点离超平面的距离最大。从上式可以看到当w w w
{ w T x i + b ⩾ 1 , y i = 1 w T x i + b ⩽ − 1 , y i = − 1 \begin{cases}
w^Tx_i + b \geqslant 1, y_i = 1 \\
w^Tx_i + b \leqslant -1, y_i = -1
\end{cases}
{ w T x i + b ⩾ 1 , y i = 1 w T x i + b ⩽ − 1 , y i = − 1
距离超平面最近的几个训练样本点使得上式的等号成立,他们被称为“支持向量”(support vector),两个异类支持向量到超平面的距离之和为
γ = 2 ∣ ∣ w ∣ ∣ \gamma = \frac{2}{||w||}
γ = ∣ ∣ w ∣ ∣ 2
于是支持向量机的基本模型就可以表示为
min w , b 1 2 ∥ w ∥ 2 s . t . y i ( w T + b ) ⩾ 1 , i = 1 , 2 , … , m \begin{array}{l}
\min _{w, b} \frac{1}{2}\|w\|^{2} \\
\text { s.t. } y_{i}\left(w^{T}+b\right) \geqslant 1, i=1,2, \ldots, m
\end{array}
w , b min 2 1 ∥ w ∥ 2 s . t . y i ( w T + b ) ⩾ 1 , i = 1 , 2 , … , m
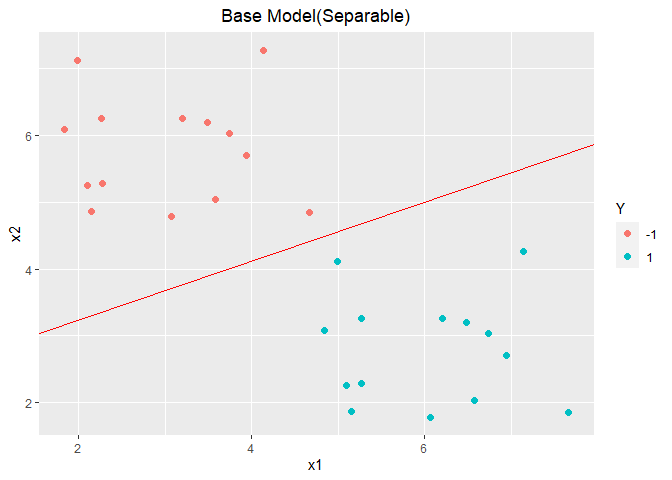
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 X <- as.matrix(data1.train[, 1 :2 ]) Y <- as.matrix(as.numeric (as.character (data1.train[, 3 ]))) SVMbase <- function (X, Y){ n <- ncol(X) m <- nrow(Y) w <- Variable(n) b <- Variable(1 ) objective <- Minimize(1 /2 * norm(w, "F" )^2 ) constraints <- list (Y * (X %*% w + b) >= 1 ) prob <- Problem(objective, constraints) solution <- solve(prob) w_res <- solution$getValue(w) b_res <- solution$getValue(b) return (list (w_res = w_res, b_res = b_res)) } modelbase <- SVMbase(X, Y) w_res <- modelbase$w_res b_res <- modelbase$b_res ggplot(data = data1.train, aes(x = x1, y = x2, colour = Y)) + geom_point(size = 2.0 , shape = 16 ) + geom_abline(slope = -w_res[1 ]/w_res[2 ], intercept = -b_res/w_res[2 ], colour = "red" ) + labs(title="Base Model(Separable)" ) + theme(plot.title = element_text(hjust = 0.5 ))
1 2 3 4 5 6 7 8 9 10 11 12 13 predictbase <- function (da, w_res, b_res){ n <- ncol(da) m <- nrow(da) X <- as.matrix(da[, 1 :(n-1 )]) preY <- X %*% w_res + b_res preY <- ifelse(preY >= 0 , 1 , -1 ) TY <- da[, 3 ] print(table(preY, TY)) return (preY) } preY <- predictbase(data1.test, w_res, b_res)
## TY
## preY -1 1
## -1 6 0
## 1 0 6
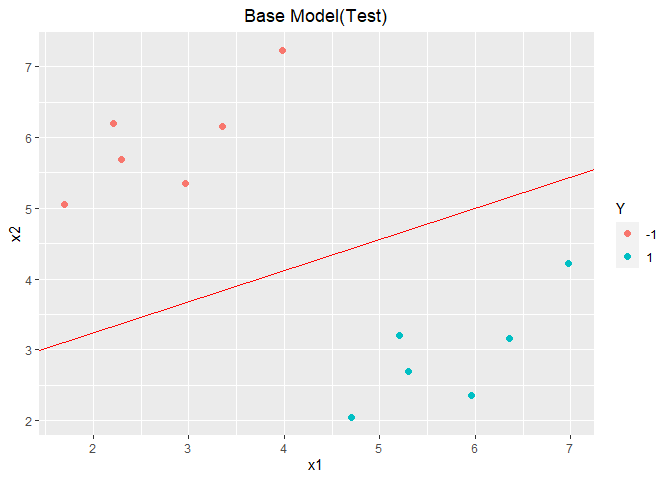
1 2 3 4 ggplot(data = data1.test, aes(x = x1, y = x2, colour = Y)) + geom_point(size = 2.0 , shape = 16 ) + geom_abline(slope = -w_res[1 ]/w_res[2 ], intercept = -b_res/w_res[2 ], colour = "red" ) + labs(title="Base Model(Test)" ) + theme(plot.title = element_text(hjust = 0.5 ))
引入拉格朗日乘子α i ⩾ 0 , i = 1 , 2 , . . . , m \alpha_i \geqslant0, i=1,2,...,m α i ⩾ 0 , i = 1 , 2 , . . . , m
L ( w , b , α ) = 1 2 ∣ ∣ w ∣ ∣ 2 + ∑ i = 1 m α i ( 1 − y i ( w T x i + b ) ) L(w,b,\alpha)=\frac{1}{2}||w||^2 + \sum_{i=1}^m\alpha_i(1-y_i(w^Tx_i + b))
L ( w , b , α ) = 2 1 ∣ ∣ w ∣ ∣ 2 + i = 1 ∑ m α i ( 1 − y i ( w T x i + b ) )
根据拉格朗日对偶性,原始问题的对偶问题是极大极小问题:
max α min w , b L ( w , b , α ) \max _{\alpha} \min _{w, b} L(w, b, \alpha)
α max w , b min L ( w , b , α )
令L ( w , b , α ) L(w,b,\alpha) L ( w , b , α ) w w w b b b
w = ∑ i = 1 m α i y i x i w=\sum_{i=1}^m \alpha_iy_ix_i
w = i = 1 ∑ m α i y i x i
0 = ∑ i = 1 m α i y i 0=\sum_{i=1}^m\alpha_iy_i
0 = i = 1 ∑ m α i y i
将上式代入拉格朗日函数得:
L ( w , b , α ) = ∑ i = 1 m α i − 1 2 ∑ i = 1 m ∑ j = 1 m α i α j y i y j x i T x j L(w,b,\alpha)=\sum_{i=1}^m \alpha_i - \frac{1}{2}\sum_{i=1}^m\sum_{j=1}^m \alpha_i\alpha_jy_iy_jx_i^Tx_j
L ( w , b , α ) = i = 1 ∑ m α i − 2 1 i = 1 ∑ m j = 1 ∑ m α i α j y i y j x i T x j
最终得到对偶问题为:
min α 1 2 ∑ i = 1 m ∑ j = 1 m α i α j y i y j x i T x j − ∑ i = 1 m α i s . t . ∑ i = 1 m α i y i = 0 α i ⩾ 0 , i = 1 , 2 , … , m \begin{array}{ll}
\min _{\alpha} & \frac{1}{2} \sum_{i=1}^{m} \sum_{j=1}^{m} \alpha_{i} \alpha_{j} y_{i} y_{j} x_{i}^{T} x_{j}-\sum_{i=1}^{m} \alpha_{i} \\
\\
\text { s.t. } & \sum_{i=1}^{m} \alpha_{i} y_{i}=0 \\
& \alpha_{i} \geqslant 0, \quad i=1,2, \ldots, m
\end{array}
α min s . t . 2 1 i = 1 ∑ m j = 1 ∑ m α i α j y i y j x i T x j − i = 1 ∑ m α i i = 1 ∑ m α i y i = 0 α i ⩾ 0 , i = 1 , 2 , … , m
对于线性可分的数据集,假设对偶问题的解为α ⋆ \alpha^\star α ⋆
w ⋆ = ∑ i = 1 m α i ⋆ y i x i w^\star=\sum_{i=1}^m \alpha^\star_iy_ix_i
w ⋆ = i = 1 ∑ m α i ⋆ y i x i
b ⋆ = y j − ∑ i = 1 m α i ⋆ y i ( x i T x j ) b^\star=y_j - \sum_{i=1}^m \alpha_i^\star y_i (x_i^T x_j)
b ⋆ = y j − i = 1 ∑ m α i ⋆ y i ( x i T x j )
b ⋆ b^\star b ⋆ j j j α \alpha α
最终原始超平面可以表示为:
∑ i = 1 m α i y i x i T x + b = 0 \sum_{i=1}^m \alpha_iy_i x_i^T x + b = 0
i = 1 ∑ m α i y i x i T x + b = 0
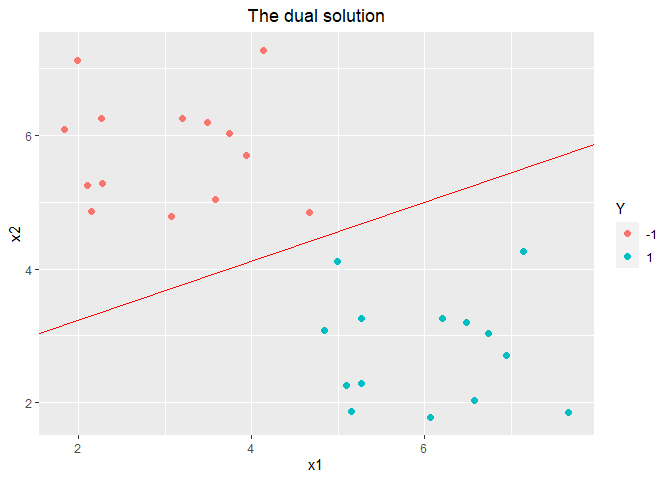
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 X <- as.matrix(data1.train[, 1 :2 ]) Y <- as.matrix(as.numeric (as.character (data1.train[, 3 ]))) SVMdual <- function (X, Y){ n <- ncol(X) m <- nrow(Y) A <- Variable(m) objective <- Minimize(-sum (A) + 1 /2 * quad_form(Y * A, X %*%t(X))) constraints <- list (A >= 0 , sum (Y * A) == 0 ) prob <- Problem(objective, constraints) solution <- solve(prob) A_res <- solution$getValue(A) w_res <- colSums(cbind(Y * A_res, Y * A_res) * X) ind <- which(A_res > 0.00001 )[1 ] b_res <- (1 - (Y[ind, 1 ])*(t(X[ind, ])%*%w_res)) / Y[ind, 1 ] return (list (w_res = w_res, b_res = b_res)) } modeldual <- SVMdual(X, Y) w_res <- modelbase$w_res b_res <- modelbase$b_res ggplot(data = data1.train, aes(x = x1, y = x2, colour = Y)) + geom_point(size = 2.0 , shape = 16 ) + geom_abline(slope = -w_res[1 ]/w_res[2 ], intercept = -b_res/w_res[2 ], colour = "red" ) + labs(title="The dual solution" ) + theme(plot.title = element_text(hjust = 0.5 ))
当原始样本空间不存在能正确划分两类样本的超平面时,我们需要将样本从原始空间映射到一个更高维的特征空间,使得样本在这个特征空间内线性可分。理论已经证明,如果原始空间是有限维的,那么一定存在一个高维特征空间使样本可分。
此时模型就可以写为
min α 1 2 ∑ i = 1 m ∑ j = 1 m α i α j y i y j ϕ ( x i ) T ϕ ( x j ) − ∑ i = 1 m α i s . t . ∑ i = 1 m α i y i = 0 α i ⩾ 0 , i = 1 , 2 , … , m \begin{array}{ll}
\min _{\alpha} & \frac{1}{2} \sum_{i=1}^{m} \sum_{j=1}^{m} \alpha_{i} \alpha_{j} y_{i} y_{j} \phi\left(x_{i}\right)^{T} \phi\left(x_{j}\right)-\sum_{i=1}^{m} \alpha_{i} \\
\\
\text { s.t. } & \sum_{i=1}^{m} \alpha_{i} y_{i}=0 \\
& \alpha_{i} \geqslant 0, \quad i=1,2, \ldots, m
\end{array}
α min s . t . 2 1 i = 1 ∑ m j = 1 ∑ m α i α j y i y j ϕ ( x i ) T ϕ ( x j ) − i = 1 ∑ m α i i = 1 ∑ m α i y i = 0 α i ⩾ 0 , i = 1 , 2 , … , m
直接计算ϕ ( x i ) T ϕ ( x j ) \phi(x_i)^T\phi(x_j) ϕ ( x i ) T ϕ ( x j )
k ( x i , x j ) = ϕ ( x i ) T ϕ ( x j ) k(x_i,x_j)=\phi(x_i)^T\phi(x_j)
k ( x i , x j ) = ϕ ( x i ) T ϕ ( x j )
常用核函数有线性核与高斯核函数,其中高斯核函数的表达式为:
k ( x i , x j ) = e x p ( − ∣ ∣ x i − x j ∣ ∣ 2 2 σ 2 ) k(x_i,x_j)=exp(-\frac{||x_i - x_j||^2}{2\sigma^2})
k ( x i , x j ) = e x p ( − 2 σ 2 ∣ ∣ x i − x j ∣ ∣ 2 )
其中σ > 0 \sigma>0 σ > 0
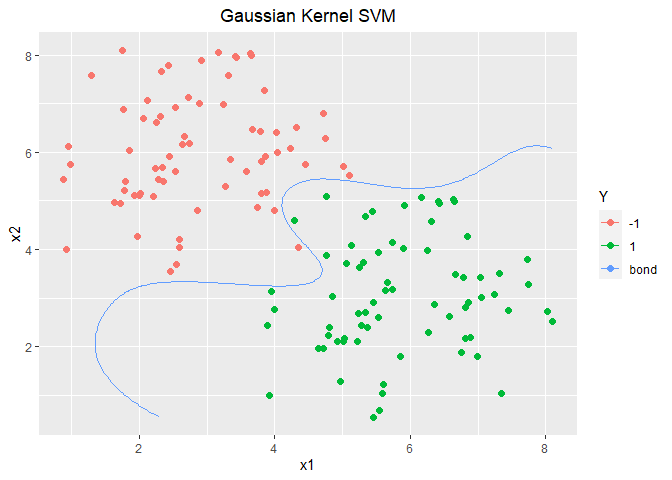
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 X <- as.matrix(data2.train[, 1 :2 ]) Y <- as.matrix(as.numeric (as.character (data2.train[, 3 ]))) GaussianK <- function (xi, xj, Sigma = 1 ){ temp <- exp (-sum ((xi - xj)^2 )/(2 * Sigma^2 )) return (temp) } SVMGaussiank <- function (X, Y, Sigma = 1 ){ n <- ncol(X) m <- nrow(Y) A <- Variable(m) KernelM <- matrix(0 , m, m) for (i in 1 :m){ for (j in 1 :m){ KernelM[i, j] <- GaussianK(X[i, ], X[j, ], Sigma) } } objective <- Minimize(-sum (A) + 1 /2 * quad_form(Y * A, KernelM)) constraints <- list (A >= 0 , sum (Y * A) == 0 ) prob <- Problem(objective, constraints) solution <- solve(prob) A_res <- solution$getValue(A) ind <- which(A_res > 0.00001 )[1 ] b_res <- Y[ind, 1 ] - sum (A_res * Y * KernelM[, ind]) return (list (A_res = A_res, b_res = b_res, X = X, Y = Y, Sigma = Sigma)) } modelGauss <- SVMGaussiank(X, Y, 1 ) PredictGauss <- function (newda, modelGauss){ A_res <- modelGauss$A_res b_res <- modelGauss$b_res X <- modelGauss$X Y <- modelGauss$Y Sigma <- modelGauss$Sigma newX <- as.matrix(newda[, 1 :2 ]) newY <- newda[, 3 ] newm <- nrow(newda) m <- nrow(X) KernelM <- matrix(0 , m, newm) for (i in 1 :m){ for (j in 1 :newm){ KernelM[i, j] <- GaussianK(X[i, ], newX[j, ], Sigma) } } preYvalue <- colSums(matrix(rep (A_res * Y, newm), ncol = newm) * KernelM) + b_res preSign <- ifelse(preYvalue >= 0 , 1 , -1 ) tb <- table(preSign, newY) return (list (preYvalue = preYvalue, preSign = preSign, tb = tb)) } PreGauss.train <- PredictGauss(data2.train, modelGauss) PreGauss.train$tb
## newY
## preSign -1 1
## -1 70 0
## 1 0 70
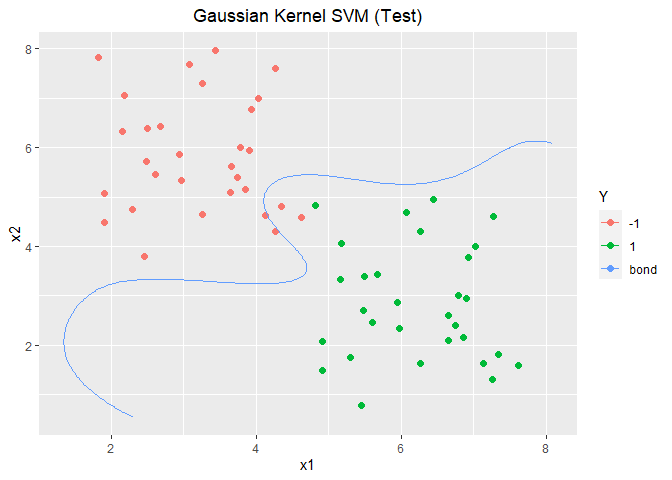
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 Wherefx0 <- function (modelGauss){ X <- modelGauss$X Sigma <- modelGauss$Sigma x1 <- seq(min (X[, 1 ]), max (X[, 1 ]),0.05 ) x2 <- seq(min (X[, 2 ]), max (X[, 2 ]),0.05 ) newda <- outer(x1, x2) colnames(newda) <- x2 rownames(newda) <- x1 newda <- melt(newda) newda$value <- 0 colnames(newda) <- c ("x1" , "x2" , "Y" ) Pred <- PredictGauss(newda, modelGauss) newda$Y <- Pred$preYvalue return (newda) } fx0 <- Wherefx0(modelGauss) ggplot(data = data2.train, aes(x = x1, y = x2, colour = Y)) + geom_point(size = 2.0 , shape = 16 ) + labs(title="Gaussian Kernel SVM" ) + theme(plot.title = element_text(hjust = 0.5 )) + stat_contour(data = fx0, aes(x = x1, y = x2, z = Y, colour = "bond" ), breaks=c (0 ))
1 2 3 PreGauss.test <- PredictGauss(data2.test, modelGauss) PreGauss.test$tb
## newY
## preSign -1 1
## -1 28 0
## 1 2 30
1 2 3 4 5 ggplot(data = data2.test, aes(x = x1, y = x2, colour = Y)) + geom_point(size = 2.0 , shape = 16 ) + labs(title="Gaussian Kernel SVM (Test)" ) + theme(plot.title = element_text(hjust = 0.5 )) + stat_contour(data = fx0, aes(x = x1, y = x2, z = Y, colour = "bond" ), breaks=c (0 ))
当样本空间线性不可分时,我们除了引入核函数的方法以外,还可以利用软间隔与正则化。软间隔(soft margin)的思想是允许支持向量机在一些样本上出错。软间隔允许某些样本不满足约束y i ( w T x i + b ) ⩾ 1 y_i(w^Tx_i + b) \geqslant 1 y i ( w T x i + b ) ⩾ 1
min w , b 1 2 ∥ w ∥ 2 + C ∑ i = 1 m l 0 / 1 ( y i ( w T x i + b ) − 1 ) \min w, b \frac{1}{2}\|w\|^{2}+C \sum_{i=1}^{m} l_{0 / 1}\left(y_{i}\left(w^{T} x_{i}+b\right)-1\right)
min w , b 2 1 ∥ w ∥ 2 + C i = 1 ∑ m l 0 / 1 ( y i ( w T x i + b ) − 1 )
其中C > 0 C>0 C > 0 l 0 / 1 l_{0/1} l 0 / 1
l 0 / 1 = { 1 , i f z < 0 0 , o t h e r w i s e l_{0/1}=
\begin{cases}
1,\,\,\,if\,\,\,z<0 \\
0,\,\,\,otherwise
\end{cases}
l 0 / 1 = { 1 , i f z < 0 0 , o t h e r w i s e
然而,l 0 / 1 l_{0/1} l 0 / 1 l h i n g e ( z ) = m a x ( 0 , 1 − z ) l_{hinge}(z)=max(0,\, 1-z) l h i n g e ( z ) = m a x ( 0 , 1 − z )
min w , b 1 2 ∥ w ∥ 2 + C ∑ i = 1 m max ( 0 , 1 − y i ( w T x i + b ) ) \min w, b \frac{1}{2}\|w\|^{2}+C \sum_{i=1}^{m} \max \left(0,1-y_{i}\left(w^{T} x_{i}+b\right)\right)
min w , b 2 1 ∥ w ∥ 2 + C i = 1 ∑ m max ( 0 , 1 − y i ( w T x i + b ) )
引入“松弛变量”(slack variables)ξ i ⩾ 0 \xi_i\geqslant0 ξ i ⩾ 0
min w , b 1 2 ∥ w ∥ 2 + C ∑ i = 1 m ξ i s . t . y i ( w T x i + b ) ⩾ 1 − ξ i ξ i ⩾ 0 , i = 1 , 2 , … , m \begin{array}{l}
\min w, b \frac{1}{2}\|w\|^{2}+C \sum_{i=1}^{m} \xi_{i} \\
\\
\text { s.t. } \quad y_{i}\left(w^{T} x_{i}+b\right) \geqslant 1-\xi_{i} \\
\quad \xi_{i} \geqslant 0, \quad i=1,2, \ldots, m
\end{array}
min w , b 2 1 ∥ w ∥ 2 + C i = 1 ∑ m ξ i s . t . y i ( w T x i + b ) ⩾ 1 − ξ i ξ i ⩾ 0 , i = 1 , 2 , … , m
这就是常见的“软间隔支持向量机”。
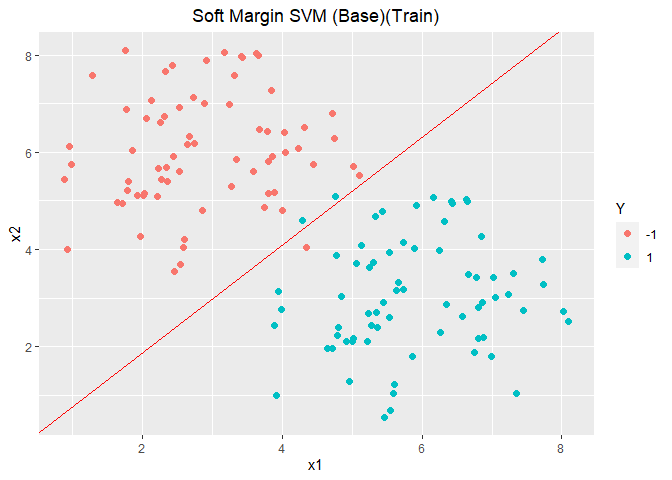
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 X <- as.matrix(data2.train[, 1 :2 ]) Y <- as.matrix(as.numeric (as.character (data2.train[, 3 ]))) SVMSoftMargin <- function (X, Y, C = 1 ){ n <- ncol(X) m <- nrow(Y) w <- Variable(n) b <- Variable(1 ) xi <- Variable(m) objective <- Minimize(1 /2 * norm(w, "F" )^2 + C*sum (xi)) constraints <- list (xi >= 0 , Y * (X %*% w + b) >= 1 -xi) prob <- Problem(objective, constraints) solution <- solve(prob) w_res <- solution$getValue(w) b_res <- solution$getValue(b) return (list (w_res = w_res, b_res = b_res)) } modelsoftmargin <- SVMSoftMargin(X, Y, C = 1 ) w_res <- modelsoftmargin$w_res b_res <- modelsoftmargin$b_res ggplot(data = data2.train, aes(x = x1, y = x2, colour = Y)) + geom_point(size = 2.0 , shape = 16 ) + geom_abline(slope = -w_res[1 ]/w_res[2 ], intercept = -b_res/w_res[2 ], colour = "red" ) + labs(title="" ) + theme(plot.title = element_text(hjust = 0.5 )) + labs(title="Soft Margin SVM (Base)(Train)" ) + theme(plot.title = element_text(hjust = 0.5 ))
1 preY <- predictbase(data2.test, w_res, b_res)
## TY
## preY -1 1
## -1 28 0
## 1 2 30
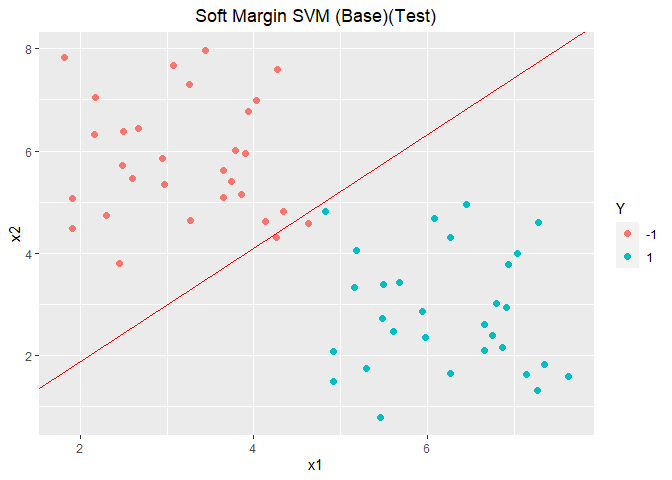
1 2 3 4 ggplot(data = data2.test, aes(x = x1, y = x2, colour = Y)) + geom_point(size = 2.0 , shape = 16 ) + geom_abline(slope = -w_res[1 ]/w_res[2 ], intercept = -b_res/w_res[2 ], colour = "red" ) + labs(title="Soft Margin SVM (Base)(Test)" ) + theme(plot.title = element_text(hjust = 0.5 ))
通过拉格朗日乘子法可将此问题转化为对偶问题
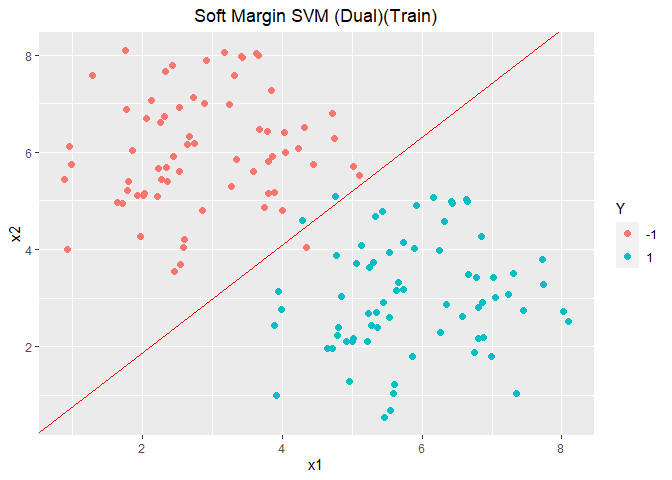
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 X <- as.matrix(data2.train[, 1 :2 ]) Y <- as.matrix(as.numeric (as.character (data2.train[, 3 ]))) SVMSoftMarginDual <- function (X, Y, C = 1 ){ n <- ncol(X) m <- nrow(Y) A <- Variable(m) objective <- Minimize(-sum (A) + 1 /2 * quad_form(Y * A, X %*%t(X))) constraints <- list (A >= 0 , A <= C, sum (Y * A) == 0 ) prob <- Problem(objective, constraints) solution <- solve(prob) A_res <- solution$getValue(A) w_res <- colSums(cbind(Y * A_res, Y * A_res) * X) ind <- which(A_res > 0.00001 ) b_res <- min (1 - (Y[ind, 1 ])*(X[ind, ]%*%w_res)) return (list (w_res = w_res, b_res = b_res)) } modelSoftMDual <- SVMSoftMarginDual(X, Y) w_res <- modelSoftMDual$w_res b_res <- modelSoftMDual$b_res ggplot(data = data2.train, aes(x = x1, y = x2, colour = Y)) + geom_point(size = 2.0 , shape = 16 ) + geom_abline(slope = -w_res[1 ]/w_res[2 ], intercept = -b_res/w_res[2 ], colour = "red" ) + labs(title="Soft Margin SVM (Dual)(Train)" ) + theme(plot.title = element_text(hjust = 0.5 ))
当然基于高斯核函数的支持向量机也可以加入软间隔降低模型过拟合的可能。
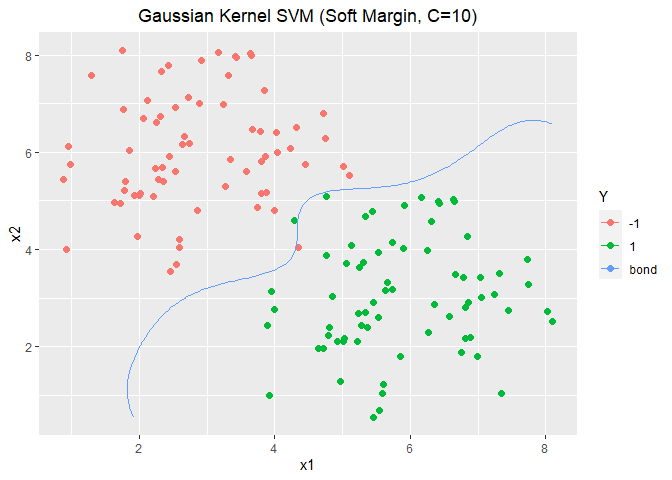
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 X <- as.matrix(data2.train[, 1 :2 ]) Y <- as.matrix(as.numeric (as.character (data2.train[, 3 ]))) SVMGaussiankSoftMargin <- function (X, Y, Sigma = 1 , C = 1 ){ n <- ncol(X) m <- nrow(Y) A <- Variable(m) KernelM <- matrix(0 , m, m) for (i in 1 :m){ for (j in 1 :m){ KernelM[i, j] <- GaussianK(X[i, ], X[j, ], Sigma) } } objective <- Minimize(-sum (A) + 1 /2 * quad_form(Y * A, KernelM)) constraints <- list (A >= 0 , A <= C, sum (Y * A) == 0 ) prob <- Problem(objective, constraints) solution <- solve(prob) A_res <- solution$getValue(A) ind <- which(A_res > 0.00001 ) b_res <- min (1 - (Y[ind, 1 ])* colSums(matrix(rep (A_res * Y, length (ind)), ncol = length (ind)) * KernelM[, ind])) return (list (A_res = A_res, b_res = b_res, X = X, Y = Y, Sigma = Sigma)) } modelGauss <- SVMGaussiankSoftMargin(X, Y, 1 , 10 ) PreGauss.train <- PredictGauss(data2.train, modelGauss) PreGauss.train$tb
## newY
## preSign -1 1
## -1 69 1
## 1 1 69
1 2 3 4 5 6 7 fx0 <- Wherefx0(modelGauss) ggplot(data = data2.train, aes(x = x1, y = x2, colour = Y)) + geom_point(size = 2.0 , shape = 16 ) + labs(title="Gaussian Kernel SVM (Soft Margin, C=10)" ) + theme(plot.title = element_text(hjust = 0.5 )) + stat_contour(data = fx0, aes(x = x1, y = x2, z = Y, colour = "bond" ), breaks=c (0 ))
我们利用OvR训练N个分类器解决支持向量机多分类问题。OvR每次将一个类的样本作为正例、所有其他类的样本作为反例来进行训练,训练完成后分别计算各分类器的f ( x ) f(x) f ( x ) f ( x ) f(x) f ( x )
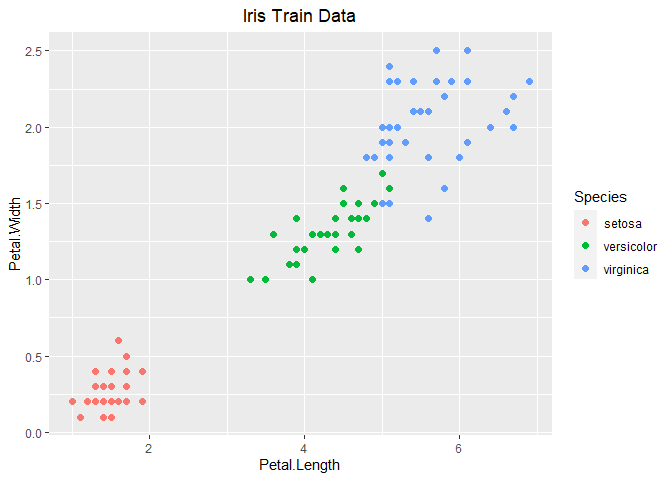
1 2 3 4 5 6 7 set.seed(1 ) ind <- sample(1 :150 , 100 ) iris.train <- iris[ind, c (3 :5 )] iris.test <- iris[c (1 :150 )[-ind], c (3 :5 )] ggplot(data = iris.train, aes(x = Petal.Length, y = Petal.Width, colour = Species)) + geom_point(size = 2.0 , shape = 16 ) + labs(title="Iris Train Data" ) + theme(plot.title = element_text(hjust = 0.5 ))
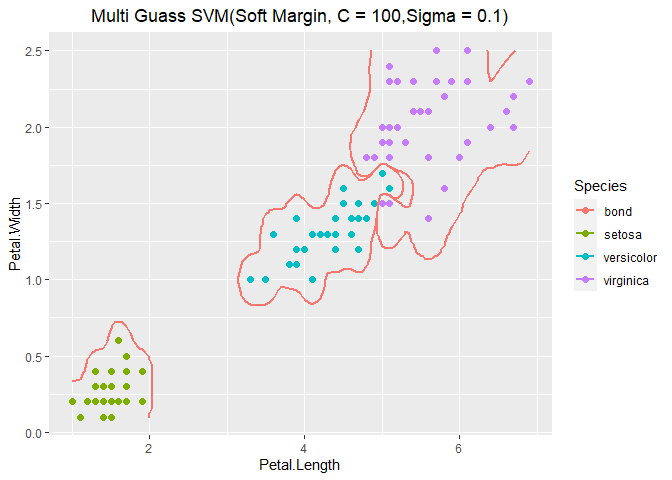
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 MultiGuassSVM <- function (da, Sigma = 1 , C = 10000 ){ m <- nrow(da) n <- ncol(da) label <- levels(da[, ncol(da)]) N <- length (label) X <- as.matrix(da[, 1 :(n-1 )]) fxdata <- data.frame(matrix(0 , ncol = N, nrow = m)) modellist <- list () for (i in 1 :N){ labeli <- label[i] Yi <- ifelse(da[, ncol(da)] == labeli, 1 , -1 ) Yi <- matrix(Yi, ncol = 1 ) dai <- da dai[, ncol(dai)] <- Yi modeli <- SVMGaussiankSoftMargin(X, Yi, Sigma, C) PreGaussi <- PredictGauss(dai, modeli) fxdata[, i] <- PreGaussi$preYvalue modellist[[i]] <- modeli } Presign <- apply(fxdata, 1 , function (x){order(x, decreasing=T )[1 ]}) Presign <- label[Presign] return (list (modellist = modellist, Presign = Presign, fxdata = fxdata, label = label, tb = table(Presign, True = da[, ncol(da)]))) } modelMultSVM <- MultiGuassSVM(iris.train, Sigma = 0.1 , C = 100 ) modelMultSVM$tb
## True
## Presign setosa versicolor virginica
## setosa 34 0 0
## versicolor 0 31 0
## virginica 0 0 35
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 fx01 <- Wherefx0(modelMultSVM$modellist[[1 ]]) fx02 <- Wherefx0(modelMultSVM$modellist[[2 ]]) fx03 <- Wherefx0(modelMultSVM$modellist[[3 ]]) ggplot(data = iris.train, aes(x = Petal.Length, y = Petal.Width, colour = Species)) + geom_point(size = 2.0 , shape = 16 ) + labs(title="Multi Guass SVM(Soft Margin, C = 100,Sigma = 0.1)" ) + theme(plot.title = element_text(hjust = 0.5 )) + stat_contour(data = fx01, aes(x = x1, y = x2, z = Y, colour = "bond" ), breaks=c (0 ), size = 1 ) + stat_contour(data = fx02, aes(x = x1, y = x2, z = Y, colour = "bond" ), breaks=c (0 ), size = 1 ) + stat_contour(data = fx03, aes(x = x1, y = x2, z = Y, colour = "bond" ), breaks=c (0 ), size = 1 )
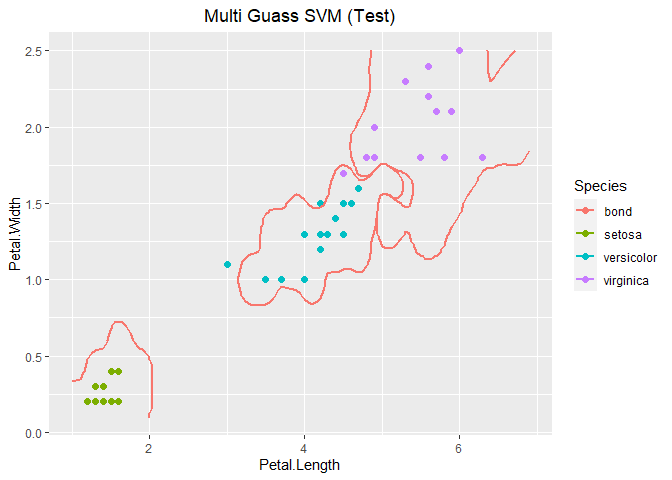
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 PredictMultiGuass <- function (da, modellist, label){ m <- nrow(da) n <- ncol(da) N <- length (modellist) X <- as.matrix(da[, 1 :(n-1 )]) fxdata <- data.frame(matrix(0 , ncol = N, nrow = m)) for (i in 1 :N){ modeli <- modellist[[i]] PreGaussi <- PredictGauss(da, modeli) fxdata[, i] <- PreGaussi$preYvalue } Presign <- apply(fxdata, 1 , function (x){order(x, decreasing=T )[1 ]}) Presign <- label[Presign] return (list (Presign = Presign, tb = table(Presign, True = da[, ncol(da)]))) } PredMultiGUass <- PredictMultiGuass(iris.test, modelMultSVM$modellist, modelMultSVM$label) PredMultiGUass$tb
## True
## Presign setosa versicolor virginica
## setosa 16 0 0
## versicolor 0 17 1
## virginica 0 2 14
1 2 3 4 5 6 7 8 9 10 11 ggplot(data = iris.test, aes(x = Petal.Length, y = Petal.Width, colour = Species)) + geom_point(size = 2.0 , shape = 16 ) + labs(title="Multi Guass SVM (Test)" ) + theme(plot.title = element_text(hjust = 0.5 )) + stat_contour(data = fx01, aes(x = x1, y = x2, z = Y, colour = "bond" ), breaks=c (0 ), size = 1 ) + stat_contour(data = fx02, aes(x = x1, y = x2, z = Y, colour = "bond" ), breaks=c (0 ), size = 1 ) + stat_contour(data = fx03, aes(x = x1, y = x2, z = Y, colour = "bond" ), breaks=c (0 ), size = 1 )
支持向量回归(Support Vector Regression,简称SVR)与传统模型不同的是,它假设我们能容忍f ( x ) f(x) f ( x ) y y y ϵ \epsilon ϵ f ( x ) f(x) f ( x ) y y y ϵ \epsilon ϵ
支持向量机回归的优化问题可以用下式表达
min w , b , ξ i c , ξ i 2 1 2 ∥ w ∥ 2 + C ∑ i = 1 m ( ξ i 1 + ξ i 2 ) s . t . f ( x i ) − y i ⩽ ϵ + ξ i 1 y i − f ( x i ) ⩽ ϵ + ξ i 2 ξ i 1 ⩾ 0 , ξ i 2 ⩾ 0 , i = 1 , 2 , … , m \begin{array}{l}
\min _{w, b, \xi_{i}^{c}, \xi_{i}^{2}} \frac{1}{2}\|w\|^{2}+C \sum_{i=1}^{m}\left(\xi_{i}^{1}+\xi_{i}^{2}\right) \\
\\
\text { s.t. } f\left(x_{i}\right)-y_{i} \leqslant \epsilon+\xi_{i}^{1} \\
\quad \quad y_{i}-f\left(x_{i}\right) \leqslant \epsilon+\xi_{i}^{2} \\
\quad \quad \xi_{i}^{1} \geqslant 0, \xi_{i}^{2} \geqslant 0, \quad i=1,2, \ldots, m
\end{array}
w , b , ξ i c , ξ i 2 min 2 1 ∥ w ∥ 2 + C i = 1 ∑ m ( ξ i 1 + ξ i 2 ) s . t . f ( x i ) − y i ⩽ ϵ + ξ i 1 y i − f ( x i ) ⩽ ϵ + ξ i 2 ξ i 1 ⩾ 0 , ξ i 2 ⩾ 0 , i = 1 , 2 , … , m
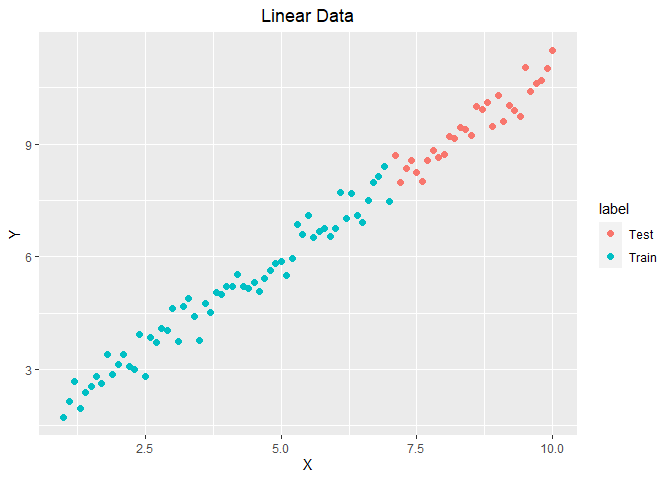
1 2 3 4 5 6 7 8 9 10 X <- seq(1 , 10 , 0.1 ) set.seed(2 ) Y <- X + 1 + rnorm(length (X), 0 , 0.3 ) linerda <- data.frame(X = X, Y = Y, label = c (rep ("Train" , 61 ), rep ("Test" , 30 ))) linerda.train <- linerda[1 :61 , 1 :2 ] linerda.test <- linerda[62 :91 , 1 :2 ] ggplot(data = linerda, aes(x = X, y = Y, colour = label)) + geom_point(size = 2 , shape = 16 ) + labs(title = "Linear Data" ) + theme(plot.title = element_text(hjust = 0.5 ))
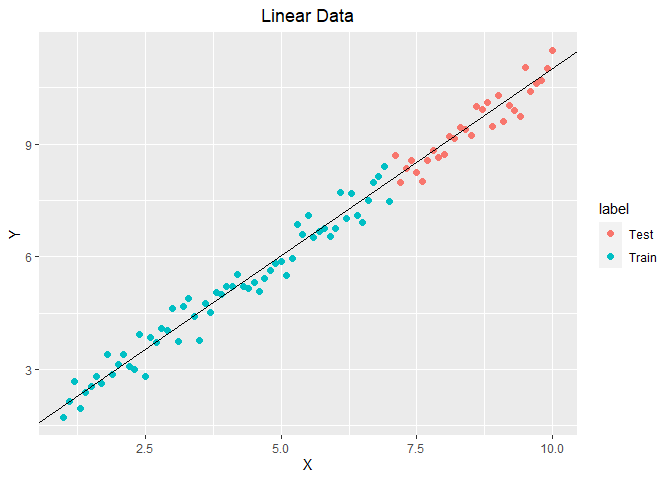
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 SVRbase <- function (da, epsilon = 0.3 , C = 1 ){ n <- ncol(da) m <- nrow(da) X <- as.matrix(da[, 1 :(n-1 )], nrow = m) Y <- as.matrix(da[, n], nrow = m) w <- Variable(n-1 ) b <- Variable(1 ) kexi1 <- Variable(m) kexi2 <- Variable(m) objective <- Minimize(0.5 * norm(w, "F" )^2 + C * sum (kexi1 + kexi2)) constraints <- list (X %*% w + b - Y <= epsilon + kexi1, Y - (X %*% w + b) <= epsilon + kexi2, kexi1 >= 0 , kexi2 >= 0 ) prob <- Problem(objective, constraints) solution <- solve(prob) w_res <- solution$getValue(w) b_res <- solution$getValue(b) return (list (w_res = w_res, b_res = b_res)) } modelSVRbase <- SVRbase(linerda.train) w_res <- modelSVRbase$w_res b_res <- modelSVRbase$b_res ggplot(data = linerda, aes(x = X, y = Y, colour = label)) + geom_point(size = 2 , shape = 16 ) + labs(title = "Linear Data" ) + theme(plot.title = element_text(hjust = 0.5 )) + geom_abline(slope = w_res, intercept = b_res, size = 0.6 )
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 predictbaseSVR <- function (da, w_res, b_res){ n <- ncol(da) m <- nrow(da) X <- as.matrix(da[, 1 :(n-1 )], nrow = m) Y <- as.matrix(da[, n], nrow = m) PreY <- X %*% w_res + b_res SSE <- sum ((PreY - Y)^2 ) return (list (PreY = PreY, SSE = SSE)) } Prelinertest <- predictbaseSVR(linerda.test, w_res, b_res) print(paste("SSE = " , round (Prelinertest$SSE,3 )))
## [1] "SSE = 3.292"
大部分内容都是代码实现,并没有太多理论的推导。原因是我对于对偶问题的理解还不是很深刻,对于KKT条件更是知之甚少。我打算在后续学完凸优化课程后再重新推导SVM的理论部分。
在编程实现的过程中有两点经验值得记录:
当求解原始问题时,b是优化参数,直接利用CVXR中的函数getValue(b)就可以求得;当求解对偶问题时,利用α i \alpha_i α i min(1 - (Y[ind, 1])*(X[ind, ]%*%w_res))求得b(ind代表α i \alpha_i α i
利用等高线0表示分类边界,stat_contour可实现此功能。
读入西瓜数据3.0,对分类变量进行独热编码(One-hot encoding)。
1 2 3 4 wmdaorign <- read.csv(file = "Test5/西瓜数据3.0.csv" ) wmdaorign <- wmdaorign[, -1 ] dmy <- dummyVars(~., data = wmdaorign) wmda <- data.frame(predict(dmy, newdata = wmdaorign))
色泽浅白
色泽青绿
色泽乌黑
根蒂蜷缩
根蒂稍蜷
根蒂硬挺
敲声沉闷
敲声清脆
敲声浊响
0
1
0
1
0
0
0
0
1
0
0
1
1
0
0
1
0
0
0
0
1
1
0
0
0
0
1
0
1
0
1
0
0
1
0
0
1
0
0
1
0
0
0
0
1
纹理模糊
纹理清晰
纹理稍糊
脐部凹陷
脐部平坦
脐部稍凹
触感软粘
触感硬滑
密度
0
1
0
1
0
0
0
1
0.697
0
1
0
1
0
0
0
1
0.774
0
1
0
1
0
0
0
1
0.634
0
1
0
1
0
0
0
1
0.608
0
1
0
1
0
0
0
1
0.556
含糖率
好瓜否
好瓜是
0.460
0
1
0.376
0
1
0.264
0
1
0.318
0
1
0.215
0
1
神经网络或连接系统是由构成动物大脑的生物神经网络模糊地启发式计算系统。神经网络本身不是算法,而是许多不同机器学习算法的框架,它们协同工作并处理复杂的数据输入。现在神经网络已经用于各种任务,包括计算机视觉、语音识别、机器翻译、社交网络过滤,游戏板和视频游戏以及医学诊断。
激活函数为sigmoid函数的单一神经元模型就是逻辑回归模型。为了通俗易懂的推导反向传播算法,我利用最简单的逻辑回归模型实现,以下为推导过程。
X = [ x ( 1 ) , x ( 2 ) , … … , x ( m ) ] n × m Y = [ y ( 1 ) , y ( 2 ) , … … , y ( m ) ] 1 × m \begin{array}{l}
X=\left[x^{(1)}, x^{(2)}, \ldots \ldots, x^{(m)}\right]_{n \times m} \\
Y=\left[y^{(1)}, y^{(2)}, \ldots \ldots, y^{(m)}\right]_{1 \times m}
\end{array}
X = [ x ( 1 ) , x ( 2 ) , … … , x ( m ) ] n × m Y = [ y ( 1 ) , y ( 2 ) , … … , y ( m ) ] 1 × m
其中上标表示第i i i m m m n n n
W ∈ R n × 1 b ∈ R W \in R^{n\times1} \,\,\,\,\,\,\,\,\, b\in R
W ∈ R n × 1 b ∈ R
W W W n n n W W W n × 1 n \times 1 n × 1 b b b
y ^ ( i ) = σ ( W T x ( i ) + b ) \hat{y}^{(i)} = \sigma (W^Tx^{(i)}+b)
y ^ ( i ) = σ ( W T x ( i ) + b )
σ ( z ) = 1 1 + e − z \sigma (z) = \frac{1}{1 + e^{-z}}
σ ( z ) = 1 + e − z 1
L ( y ^ , y ) = − ( y l o g ( y ^ ) + ( 1 − y ) l o g ( 1 − y ^ ) ) L(\hat{y}, y) = -(ylog(\hat{y}) + (1-y)log(1-\hat{y}))
L ( y ^ , y ) = − ( y l o g ( y ^ ) + ( 1 − y ) l o g ( 1 − y ^ ) )
J ( W , b ) = 1 m ∑ i = 1 m L ( y ^ ( i ) , y ( i ) ) J(W, b)=\frac{1}{m}\sum_{i=1}^mL(\hat{y}^{(i)},y^{(i)})
J ( W , b ) = m 1 i = 1 ∑ m L ( y ^ ( i ) , y ( i ) )
我们的目标是利用梯度下降法最小化代价函数。反向传播法其实就是根据链式法则计算偏导数的,下面我们进行推导。
当n = 2 n=2 n = 2
z = w 1 x 1 + w 2 x 2 + b y ^ = a = σ ( z ) L ( a , y ) \begin{array}{l}
z=w_{1} x_{1}+w_{2} x_{2}+b \\
\\
\hat{y}=a=\sigma(z) \\
\\
L(a, y)
\end{array}
z = w 1 x 1 + w 2 x 2 + b y ^ = a = σ ( z ) L ( a , y )
d z = d L d z = d L ( a , y ) d z = d L d a d a d z = a − y dz = \frac{dL}{dz}=\frac{dL(a,y)}{dz}=\frac{dL}{da}\frac{da}{dz}=a-y
d z = d z d L = d z d L ( a , y ) = d a d L d z d a = a − y
其中
d L d a = − y a + 1 − y 1 − a \frac{dL}{da} = -\frac{y}{a} + \frac{1-y}{1-a}
d a d L = − a y + 1 − a 1 − y
d a d z = a ( 1 − a ) \frac{da}{dz} = a(1-a)
d z d a = a ( 1 − a )
显然
d L d w 1 = x 1 d z = x 1 ( a − y ) d L d w 2 = x 2 d z = x 2 ( a − y ) d b = d z = a − y \begin{aligned}
\frac{d L}{d w_{1}} &=x_{1} d z=x_{1}(a-y) \\
\frac{d L}{d w_{2}} &=x_{2} d z=x_{2}(a-y) \\
d b &=d z=a-y
\end{aligned}
d w 1 d L d w 2 d L d b = x 1 d z = x 1 ( a − y ) = x 2 d z = x 2 ( a − y ) = d z = a − y
当n = 2 n=2 n = 2 m m m for循环计算m m m
d Z = [ d z ( 1 ) , d z ( 2 ) , … … , d z ( m ) ] A = [ a ( 1 ) , a ( 2 ) , … … , a ( m ) ] \begin{aligned}
d Z &=\left[d z^{(1)}, d z^{(2)}, \ldots \ldots, d z^{(m)}\right] \\
A &=\left[a^{(1)}, a^{(2)}, \ldots \ldots, a^{(m)}\right]
\end{aligned}
d Z A = [ d z ( 1 ) , d z ( 2 ) , … … , d z ( m ) ] = [ a ( 1 ) , a ( 2 ) , … … , a ( m ) ]
d Z = A − Y dZ=A-Y
d Z = A − Y
则
d W = 1 m X d Z T dW = \frac{1}{m}X\,dZ^T
d W = m 1 X d Z T
d b = 1 m ∑ i = 1 m d Z ( i ) db = \frac{1}{m} \sum_{i=1}^mdZ^{(i)}
d b = m 1 i = 1 ∑ m d Z ( i )
根据上一节的推导过程,我们推导了单隐层神经网络向前传播求Y ^ \hat{Y} Y ^
上角标[ i ] ^{[i]} [ i ] i i i i i i
Z [ 1 ] = W [ 1 ] X + b [ 1 ] A [ 1 ] = σ ( Z [ 1 ] ) Z [ 2 ] = W [ 2 ] A [ 1 ] + b [ 2 ] A [ 2 ] = σ ( Z [ 2 ] ) \begin{array}{l}
Z^{[1]}=W^{[1]} X+b^{[1]} \\
A^{[1]}=\sigma\left(Z^{[1]}\right) \\
Z^{[2]}=W^{[2]} A^{[1]}+b^{[2]} \\
A^{[2]}=\sigma\left(Z^{[2]}\right)
\end{array}
Z [ 1 ] = W [ 1 ] X + b [ 1 ] A [ 1 ] = σ ( Z [ 1 ] ) Z [ 2 ] = W [ 2 ] A [ 1 ] + b [ 2 ] A [ 2 ] = σ ( Z [ 2 ] )
其中W [ i ] W^{[i]} W [ i ] i − 1 i-1 i − 1 i i i l [ i ] × l [ i − 1 ] l^{[i]} \times l^{[i-1]} l [ i ] × l [ i − 1 ] l l l
d Z [ 2 ] = A [ 2 ] − Y d W [ 2 ] = 1 m d Z [ 2 ] A [ 1 ] T d b [ 2 ] = 1 m ∑ i = 1 m d Z ( i ) [ 2 ] d Z [ 1 ] = W [ 2 ] T d Z [ 2 ] ∗ g [ 1 ] ′ ( Z [ 1 ] ) d W [ 1 ] = 1 m d Z [ 1 ] X T d b [ 1 ] = 1 m ∑ i = 1 m d Z ( i ) [ 1 ] \begin{aligned}
d Z^{[2]} &=A^{[2]}-Y \\
d W^{[2]} &=\frac{1}{m} d Z^{[2]} A^{[1] T} \\
d b^{[2]} &=\frac{1}{m} \sum_{i=1}^{m} d Z_{(i)}^{[2]} \\
d Z^{[1]} &=W^{[2] T} d Z^{[2]} * g^{[1]^{\prime}}\left(Z^{[1]}\right) \\
d W^{[1]} &=\frac{1}{m} d Z^{[1]} X^{T} \\
d b^{[1]} &=\frac{1}{m} \sum_{i=1}^{m} d Z_{(i)}^{[1]}
\end{aligned}
d Z [ 2 ] d W [ 2 ] d b [ 2 ] d Z [ 1 ] d W [ 1 ] d b [ 1 ] = A [ 2 ] − Y = m 1 d Z [ 2 ] A [ 1 ] T = m 1 i = 1 ∑ m d Z ( i ) [ 2 ] = W [ 2 ] T d Z [ 2 ] ∗ g [ 1 ] ′ ( Z [ 1 ] ) = m 1 d Z [ 1 ] X T = m 1 i = 1 ∑ m d Z ( i ) [ 1 ]
初始化参数时,不能像逻辑回归一样直接将W W W 0 0 0 W W W
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 InitParam <- function (nx, nh, ny, seed = 2 ){ set.seed(seed) W1 <- matrix(rnorm(nx * nh), ncol = nx) * 0.01 b1 <- matrix(rep (0 , nh), ncol = 1 ) W2 <- matrix(rnorm(ny * nh), ncol = nh) * 0.01 b2 <- matrix(rep (0 , ny), ncol = 1 ) return (list (W1 = W1, b1 = b1, W2 = W2, b2 = b2)) } InitParamDeep <- function (Ldims, seed = 2 ){ set.seed(seed) Paramlist <- list () L = length (Ldims) for (i in 2 :L){ Wi <- matrix(rnorm(Ldims[i-1 ] * Ldims[i]), ncol = Ldims[i-1 ]) * 0.01 bi <- matrix(rep (0 , Ldims[i]), ncol = 1 ) Paramlist[[i-1 ]] <- list (Wi = Wi, bi = bi) } return (Paramlist) } LinearForward <- function (A, W, b){ Z <- W %*% A + matrix(rep (b, ncol(A)), ncol = ncol(A)) return (list (Z = Z, A = A, W = W, b = b)) } sigmoid <- function (Z){ A <- 1 / (1 + exp (-Z)) return (A) } LinActForward <- function (Aprev, W, b){ templist <- LinearForward(Aprev, W, b) Z <- templist$Z A <- sigmoid(Z) return (list (Z = Z, A = A, W = W, b = b, Aprev = Aprev)) } LModelForward <- function (X, Paramlist){ cacheslist <- list () A <- X L <- length (Paramlist) for (i in 1 :L){ Aprev <- A W <- Paramlist[[i]]$W b <- Paramlist[[i]]$b templist <- LinActForward(Aprev, W, b) A <- templist$A cacheslist[[i]] <- templist } return (list (A = A, cacheslist = cacheslist)) } ComputeCost <- function (AL, Y){ m <- length (Y) cost <- -1 /m * sum (Y * log (AL) + (1 -Y) * log (1 -AL)) return (cost) } LinActBackward <- function (dA, cache){ APrev <- cache$Aprev W <- cache$W b <- cache$b Z <- cache$Z m <- ncol(APrev) s <- 1/(1 +exp (-Z)) dZ <- dA * (s * (1 - s)) dAprev <- t(W) %*% dZ dW <- 1/m * dZ %*% t(APrev) db <- 1/m * rowSums(dZ) return (list (dAprev = dAprev, dW = dW, db = db)) } LModelBackward <- function (AL, Y, cacheslist){ grads <- list () L <- length (cacheslist) m <- length (AL) dAL <- -Y/AL + (1 -Y)/(1 -AL) dA <- dAL for (i in L:1 ){ grads[[i]] <- LinActBackward(dA, cacheslist[[i]]) dA <- grads[[i]]$dAprev } return (grads) } UpdateParams <- function (Paramlist, grads, learnrate = 0.1 ){ L <- length (Paramlist) for (i in 1 :L){ Paramlist[[i]]$Wi <- Paramlist[[i]]$Wi - learnrate * grads[[i]]$dW Paramlist[[i]]$bi <- Paramlist[[i]]$bi - learnrate * grads[[i]]$db } return (Paramlist) } NNmodel <- function (X, Y, Ldims, seed = 2 , learnrate = 0.1 , numiter = 10000 , printcost = FALSE ){ costs <- vector(length = numiter) Paramlist <- InitParamDeep(Ldims, seed = seed) for (i in 1 :numiter){ Forward <- LModelForward(X, Paramlist) AL <- Forward$A cacheslist <- Forward$cacheslist cost <- ComputeCost(AL, Y) grads <- LModelBackward(AL, Y, cacheslist) Paramlist <- UpdateParams(Paramlist, grads, learnrate) if (printcost == TRUE & i%%100==0 ){ print(paste("Cost after iteration" , i, ":" , cost)) } costs[i] <- cost } return (list (Paramlist = Paramlist, costs = costs)) } NNmodelSGD <- function (X, Y, Ldims, seed = 2 , learnrate = 0.1 , numiter = 100 , printcost = FALSE ){ m <- ncol(Y) costs <- vector(length = numiter*m) Paramlist <- InitParamDeep(Ldims, seed = seed) Xall <- X Yall <- Y for (i in 1 :numiter){ for (j in 1 :m){ X <- Xall[, j, drop = FALSE ] Y <- Yall[, j, drop = FALSE ] Forward <- LModelForward(X, Paramlist) AL <- Forward$A cacheslist <- Forward$cacheslist cost <- ComputeCost(AL, Y) grads <- LModelBackward(AL, Y, cacheslist) Paramlist <- UpdateParams(Paramlist, grads, learnrate) if (printcost == TRUE & i%%100==0 ){ print(paste("Cost after iteration" , i, ":" , cost)) } costs[m*(i-1 ) + j] <- cost } } return (list (Paramlist = Paramlist, costs = costs)) } NNpredict <- function (NewX, NewY, Model){ PreY <- LModelForward(NewX, Model$Paramlist)$A PreY <- ifelse(PreY >= 0.5 , 1 , 0 ) tb <- table(PreY, NewY) accuracy <- sum (diag(tb)) / sum (tb) return (list (PreY = PreY, tb = tb, accuracy = accuracy)) }
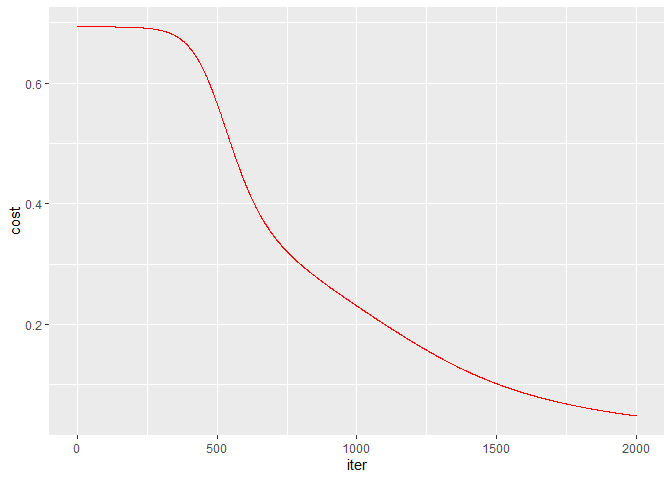
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 X <- t(as.matrix(wmda[, 1 :19 ])) Y <- t(as.matrix(wmda[, 21 ])) set.seed(seed = 1 ) ind <- sample(ncol(Y), 12 ) X.train <- X[, ind] Y.train <- Y[, ind, drop = FALSE ] X.test <- X[, -ind] Y.test <- Y[, -ind, drop = FALSE ] Model <- NNmodel(X.train, Y.train, Ldims = c (19 , 10 , 1 ), seed = 2 , learnrate = 0.1 , numiter = 2000 ) costs <- data.frame(iter = 1 :2000 , cost = Model$costs) ggplot(data = costs, aes(x = iter, y = cost)) + geom_line(color = "red" )
1 2 3 Predict.train <- NNpredict(X.train, Y.train, Model) print(paste("The Train accuracy is : " , Predict.train$accuracy * 100 , "%" ))
## [1] "The Train accuracy is : 100 %"
1 print("The confusion matrix is : " )
## [1] "The confusion matrix is : "
## NewY
## PreY 0 1
## 0 6 0
## 1 0 6
1 2 3 Predict.test <- NNpredict(X.test, Y.test, Model) print(paste("The Test accuracy is : " , Predict.test$accuracy * 100 , "%" ))
## [1] "The Test accuracy is : 20 %"
1 print("The confusion matrix is : " )
## [1] "The confusion matrix is : "
## NewY
## PreY 0 1
## 0 1 2
## 1 2 0
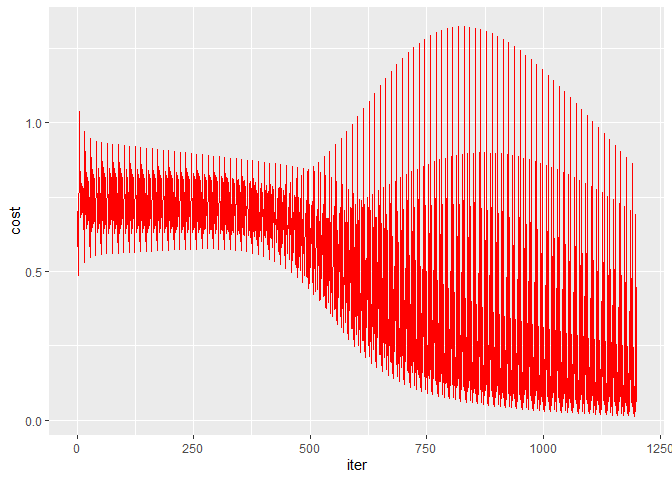
1 2 3 4 5 6 ModelSGD <- NNmodelSGD(X.train, Y.train, Ldims = c (19 , 10 , 1 ), seed = 2 , learnrate = 0.1 , numiter = 100 ) costs <- data.frame(iter = 1 :(12 * 100 ), cost = ModelSGD$costs) ggplot(data = costs, aes(x = iter, y = cost)) + geom_line(color = "red" )
1 2 3 Predict.train <- NNpredict(X.train, Y.train, ModelSGD) print(paste("The Train accuracy is : " , Predict.train$accuracy * 100 , "%" ))
## [1] "The Train accuracy is : 91.6666666666667 %"
1 print("The confusion matrix is : " )
## [1] "The confusion matrix is : "
## NewY
## PreY 0 1
## 0 6 1
## 1 0 5
1 2 3 Predict.test <- NNpredict(X.test, Y.test, ModelSGD) print(paste("The Test accuracy is : " , Predict.test$accuracy * 100 , "%" ))
## [1] "The Test accuracy is : 40 %"
1 print("The confusion matrix is : " )
## [1] "The confusion matrix is : "
## NewY
## PreY 0 1
## 0 2 2
## 1 1 0
神经网络是一个庞大的体系,本文仅展示了经典的方法——反向传播算法。后续内容可能涉及到的有如何划分训练集与测试集、方差偏差法判断模型拟合程度、正则化(L i L_i L i
读入朴素贝叶斯实验数据,并进行展示。
1 2 3 da <- read.csv("Test6/data.csv" ) da.train <- da[1 :14 , ] da.test <- da[15 , ]
No
Age
Income
Student
Credit_rating
Class.buys_computer
1
<=30
High
No
Fair
No
2
<=30
High
No
Excellent
No
3
31-40
High
No
Fair
Yes
4
>40
Medium
No
Fair
Yes
5
>40
Low
Yes
Fair
Yes
6
>40
Low
Yes
Excellent
No
7
31-40
Low
Yes
Excellent
Yes
8
<=30
Medium
No
Fair
No
9
<=30
Low
Yes
Fair
Yes
10
>40
Medium
Yes
Fair
Yes
11
<=30
Medium
Yes
Excellent
Yes
12
31-40
Medium
No
Excellent
Yes
13
31-40
High
Yes
Fair
Yes
14
>40
Medium
No
Excellent
No
15
<=30
Medium
Yes
Fair
朴素贝叶斯分类器(naive Bayes classifier)采用了“属性条件独立性假设”:对已知类别,假设所有属性相互独立。换而言之,假设每个属性独立地对分裂结果发生影响。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 naiveBayes <- function (da, Classn = 6 , Factorn = c (2 :5 )){ Class <- levels(as.factor(da[, Classn])) Pc <- vector(length = length (Class)) for (i in 1 :length (Class)){ Pc[i] <- (length (da[which(da[, Classn] == Class[i]), Classn]) + 1 )/(nrow(da) + 2 ) } Pc <- data.frame(Class = Class, P = Pc) Factorlist <- list () k <- 1 for (i in Factorn){ Classi <- levels(as.factor(da[, i])) temp <- as.data.frame(matrix(nrow = length (Classi), ncol = nrow(Pc) + 1 )) temp[, 1 ] <- Classi for (j in 1 :length (Classi)){ for (t in 1 :length (Class)){ temp[j, t + 1 ] <- (length (da[which(da[, i] == Classi[j] & da[, Classn] == Class[t]), i]) + 1 )/(length (da[which(da[, Classn] == Class[t]), i]) + length (Classi)) } } colnames(temp) <- c ("Class" , Pc$Class) Factorlist[[k]] <- temp k <- k+1 } names (Factorlist) <- colnames(da[, Factorn]) return (list (Pc = Pc, Factorlist = Factorlist)) } mymodel <- naiveBayes(da.train, 6 , c (2 :5 )) predictnB <- function (da, mymodel, Factorn = c (2 :5 )){ factors <- colnames(da[, Factorn]) Classn <- nrow(mymodel$Pc) P <- data.frame(Classn = mymodel$Pc$Class, P = 1 ) for (i in 1 :Classn){ for (j in 1 :length (factors)){ temp <- mymodel$Factorlist[factors[j]][[1 ]] ind <- which(temp$Class == da[,factors[j]]) P$P <- as.numeric (P$P * temp[ind, -1 ]) } } return (P) } knitr::kable(predictnB(da.test, mymodel, c (2 :5 )))
Classn
P
No
0.0004036
Yes
0.0014952
由上表可以看出 Yes 的概率大于 No 的概率,所以测试样本应该会买电脑。